题目内容
已知:f(x)=2cos2x+sin2x+a.(a∈R,a为常数)(1)若x∈R,求f(x)单调递增区间;
(2)若f(x)在[-
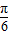 ,
,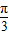 ]上最大值与最小值之和为3,求a的值;
]上最大值与最小值之和为3,求a的值;(3)在(2)条件下的f(x)与g(x)关于x=
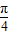 对称,写出g(x)的解析式.
对称,写出g(x)的解析式.
【答案】分析:(1)利用两角和差的正弦公式化简f(x)的解析式为2sin(2x+ )+a+1,由 2kπ-
)+a+1,由 2kπ-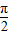 ≤2x+
≤2x+ ≤2kπ+
≤2kπ+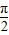 ,k∈z,求得f(x)的单调递增区间.
,k∈z,求得f(x)的单调递增区间.
(2)根据x的范围求出2x+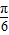 的范围,进而得到sin(2x+
的范围,进而得到sin(2x+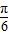 )的范围,从而得到f(x)的最大值和最小值,由最大值与最小值之和为3,求得a的值.
)的范围,从而得到f(x)的最大值和最小值,由最大值与最小值之和为3,求得a的值.
(3)由(2)可得f(x)=2sin(2x+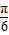 )+1,f(x)与g(x)关于x=
)+1,f(x)与g(x)关于x=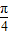 对称,可得 g(x)=f(
对称,可得 g(x)=f(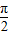 -x),利用诱导公式求得g(x)的解析式.
-x),利用诱导公式求得g(x)的解析式.
解答:解:(1)f(x)=1+cos2x+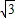 sin2x+a=2sin(2x+
sin2x+a=2sin(2x+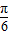 )+a+1.(2分)
)+a+1.(2分)
由 2kπ- ≤2x+
≤2x+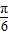 ≤2kπ+
≤2kπ+ ,k∈z,可得kπ-
,k∈z,可得kπ-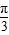 ≤x≤kπ+
≤x≤kπ+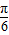 ,k∈Z,
,k∈Z,
故 f(x)的单调递增区间为[kπ- ,kπ+
,kπ+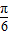 ],k∈Z.(4分)
],k∈Z.(4分)
(2)x∈[-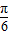 ,
,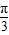 ],∴2x+
],∴2x+ ∈[-
∈[-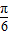 ,
,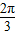 ],∴sin(2x+
],∴sin(2x+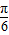 )∈[-
)∈[- ,1]).(7分)
,1]).(7分)
∴f(x)的最大值为3+a,最小值为a,∴3+a+a=3,∴a=0.(9分)
(3)由(2)可得f(x)=2sin(2x+ )+1,f(x)与g(x)关于x=
)+1,f(x)与g(x)关于x=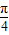 对称,
对称,
故g(x)=f(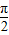 -x)=sin[2(
-x)=sin[2(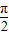 -x)+
-x)+ ]=sin(π+
]=sin(π+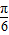 -2x)=-sin(
-2x)=-sin(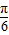 -2x)=sin(2x-
-2x)=sin(2x- ),
),
即 g(x)=sin(2x- ). (12分)
). (12分)
点评:本题主要考查两角和差的正弦公式,同角三角函数的基本关系,诱导公式,正弦函数的定义域和值域,属于中档题.
 )+a+1,由 2kπ-
)+a+1,由 2kπ-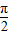 ≤2x+
≤2x+ ≤2kπ+
≤2kπ+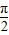 ,k∈z,求得f(x)的单调递增区间.
,k∈z,求得f(x)的单调递增区间.(2)根据x的范围求出2x+
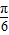 的范围,进而得到sin(2x+
的范围,进而得到sin(2x+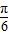 )的范围,从而得到f(x)的最大值和最小值,由最大值与最小值之和为3,求得a的值.
)的范围,从而得到f(x)的最大值和最小值,由最大值与最小值之和为3,求得a的值.(3)由(2)可得f(x)=2sin(2x+
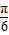 )+1,f(x)与g(x)关于x=
)+1,f(x)与g(x)关于x=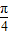 对称,可得 g(x)=f(
对称,可得 g(x)=f(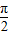 -x),利用诱导公式求得g(x)的解析式.
-x),利用诱导公式求得g(x)的解析式.解答:解:(1)f(x)=1+cos2x+
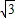 sin2x+a=2sin(2x+
sin2x+a=2sin(2x+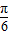 )+a+1.(2分)
)+a+1.(2分)由 2kπ-
 ≤2x+
≤2x+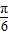 ≤2kπ+
≤2kπ+ ,k∈z,可得kπ-
,k∈z,可得kπ-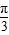 ≤x≤kπ+
≤x≤kπ+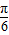 ,k∈Z,
,k∈Z,故 f(x)的单调递增区间为[kπ-
 ,kπ+
,kπ+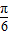 ],k∈Z.(4分)
],k∈Z.(4分)(2)x∈[-
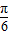 ,
,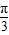 ],∴2x+
],∴2x+ ∈[-
∈[-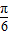 ,
,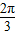 ],∴sin(2x+
],∴sin(2x+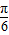 )∈[-
)∈[- ,1]).(7分)
,1]).(7分)∴f(x)的最大值为3+a,最小值为a,∴3+a+a=3,∴a=0.(9分)
(3)由(2)可得f(x)=2sin(2x+
 )+1,f(x)与g(x)关于x=
)+1,f(x)与g(x)关于x=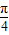 对称,
对称,故g(x)=f(
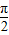 -x)=sin[2(
-x)=sin[2(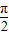 -x)+
-x)+ ]=sin(π+
]=sin(π+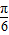 -2x)=-sin(
-2x)=-sin(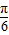 -2x)=sin(2x-
-2x)=sin(2x- ),
),即 g(x)=sin(2x-
 ). (12分)
). (12分)点评:本题主要考查两角和差的正弦公式,同角三角函数的基本关系,诱导公式,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目