题目内容
已知函数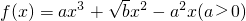 ,f'(x)是f(x)的导函数,若存在x1,x2∈R,x1<x2,且f'(x1)=f'(x2)=0,|x1|+|x2|=2.
,f'(x)是f(x)的导函数,若存在x1,x2∈R,x1<x2,且f'(x1)=f'(x2)=0,|x1|+|x2|=2.
(1)证明0<a≤3;
(2)求实数b的取值范围.
解:(1)求导,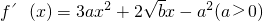 …(1分)
…(1分)
由f'(x1)=f'(x2)=0,x1、x2是方程f'(x)=0的两实根
∴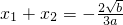 ,
,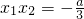
从已知 ,
,
∴|x1x2|≤1,即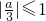
∴|a|≤3,又a>0
∴0<a≤3…(6分)
(2)∵x1<x2且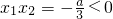
∴x1<0<x2|x1|+|x2|=-x1+x2=2
∴(x2-x1)2=(x1+x2)2-4x1x2=4
代入韦达定理关系,得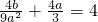
∴b=-3a3+9a2(0<a≤3)…(9分)
求导,b'=-9a2+18a=-9a(a-2)
当a∈(0,2),b'>0,b递增;
当a∈(2,3),b'<0,b递减a=2时,
∴bmax=12,又当b=3时,b=0…(11分)
∴0≤b≤12为所求.…(12分)
分析:(1)求导,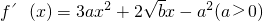 .由f'(x1)=f'(x2)=0,x1、x2是方程f'(x)=0的两实根,由此能够证明0<a≤3.
.由f'(x1)=f'(x2)=0,x1、x2是方程f'(x)=0的两实根,由此能够证明0<a≤3.
(2)由x1<x2且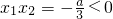 ,知x1<0<x2|x1|+|x2|=-x1+x2=2.所以(x2-x1)2=(x1+x2)2-4x1x2=4.由此能求出实数a的范围.
,知x1<0<x2|x1|+|x2|=-x1+x2=2.所以(x2-x1)2=(x1+x2)2-4x1x2=4.由此能求出实数a的范围.
点评:本题考查根与系数的关系,解题时要认真审题,仔细解答,注意合理地进行等价转化.
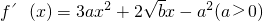 …(1分)
…(1分)由f'(x1)=f'(x2)=0,x1、x2是方程f'(x)=0的两实根
∴
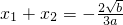 ,
,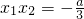
从已知
 ,
,∴|x1x2|≤1,即
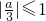
∴|a|≤3,又a>0
∴0<a≤3…(6分)
(2)∵x1<x2且
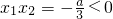
∴x1<0<x2|x1|+|x2|=-x1+x2=2
∴(x2-x1)2=(x1+x2)2-4x1x2=4
代入韦达定理关系,得
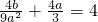
∴b=-3a3+9a2(0<a≤3)…(9分)
求导,b'=-9a2+18a=-9a(a-2)
当a∈(0,2),b'>0,b递增;
当a∈(2,3),b'<0,b递减a=2时,
∴bmax=12,又当b=3时,b=0…(11分)
∴0≤b≤12为所求.…(12分)
分析:(1)求导,
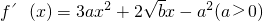 .由f'(x1)=f'(x2)=0,x1、x2是方程f'(x)=0的两实根,由此能够证明0<a≤3.
.由f'(x1)=f'(x2)=0,x1、x2是方程f'(x)=0的两实根,由此能够证明0<a≤3.(2)由x1<x2且
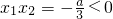 ,知x1<0<x2|x1|+|x2|=-x1+x2=2.所以(x2-x1)2=(x1+x2)2-4x1x2=4.由此能求出实数a的范围.
,知x1<0<x2|x1|+|x2|=-x1+x2=2.所以(x2-x1)2=(x1+x2)2-4x1x2=4.由此能求出实数a的范围.点评:本题考查根与系数的关系,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
