题目内容
已知0＜α＜
，且lg（1+cosα）=m，lg
=n，，则lgsinα的值为
- A.m+
- B.
（m+） - C.m-n
- D.（m-n）
D
分析：通过lg（1+cosα）=m，化简lg=n，通过两个表达式的代换，求出lgsinα的值．
解答：0＜α＜，且lg（1+cosα）=m；
又 lg=n，
=
=lg（1+cosα）-2lgsinα=n，
∴m-2lgsinα=n，
∴lgsinα=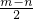
．
故选D．
点评：本题是基础题，考查三角函数的化简对数函数的基本运算，考查计算能力．
分析：通过lg（1+cosα）=m，化简lg
=n，通过两个表达式的代换，求出lgsinα的值．解答：0＜α＜
，且lg（1+cosα）=m；又 lg
=n，==lg（1+cosα）-2lgsinα=n，∴m-2lgsinα=n，
∴lgsinα=
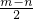．故选D．
点评：本题是基础题，考查三角函数的化简对数函数的基本运算，考查计算能力．
练习册系列答案
相关题目
,且lg (1+cosα)=m,lg
=n，则lg sinα等（ ）
B．m-nC．12(m+
)D．12(m-n)