题目内容
设a为非零常数,若函数f(x)=ax3+x在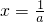 处取得极值,则a的值为
处取得极值,则a的值为
- A.-3
- B.

- C.3
- D.

A
分析:求导函数,根据函数f(x)=ax3+x在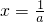 处取得极值,可得
处取得极值,可得 =0,从而可求a的值,
=0,从而可求a的值,
解答:求导函数可得f′(x)=3ax2+1
∵函数f(x)=ax3+x在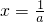 处取得极值
处取得极值
∴ =0
=0
∴a=-3
此时f′(x)=-9x2+1,函数在(-∞,- )上单调减,在(-
)上单调减,在(- ,
, )上单调增,在(
)上单调增,在( ,+∞)上单调减,函数在
,+∞)上单调减,函数在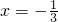 处取得极小值
处取得极小值
故选A
点评:本题考查导数知识的运用,考查函数的极值,正确求导是关键.
分析:求导函数,根据函数f(x)=ax3+x在
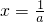 处取得极值,可得
处取得极值,可得 =0,从而可求a的值,
=0,从而可求a的值,解答:求导函数可得f′(x)=3ax2+1
∵函数f(x)=ax3+x在
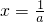 处取得极值
处取得极值∴
 =0
=0∴a=-3
此时f′(x)=-9x2+1,函数在(-∞,-
 )上单调减,在(-
)上单调减,在(- ,
, )上单调增,在(
)上单调增,在( ,+∞)上单调减,函数在
,+∞)上单调减,函数在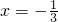 处取得极小值
处取得极小值故选A
点评:本题考查导数知识的运用,考查函数的极值,正确求导是关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目