题目内容
集合A＝{x|－2≤x≤5}，集合B＝{x|m＋1≤x≤2m－1}．
(1) 若B
A，求实数m的取值范围；
(2) 当x∈R时，没有元素x使x∈A与x∈B同时成立，求实数m的取值范围．
解：(1) 当m＋1＞2m－1即m＜2时，B＝
满足BA；
当m＋1≤2m－1即m≥2时，要使BA成立，则
解得2≤m≤3.
综上所述，当m≤3时有BA.
(2) 因为x∈R，且A＝{x|－2≤x≤5}，B＝{x|m＋1≤x≤2m－1}，又没有元素x使x∈A与x∈B同时成立，则
① 若B＝，即m＋1＞2m－1，得m＜2时满足条件；
② 若B≠，则要满足条件
解得m＞4.
或
无解．
综上所述，实数m的取值范围为m＜2或m＞4.
练习册系列答案
名校课堂系列答案
相关题目
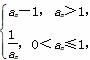则下列结论中错误的是( )
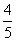，则a5＝3 B．若a3＝2，则m可以取3个不同的值
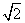，则数列{an}是周期为3的数列 D．∃m∈Q且m≥2，使得数列{an}是周期数列
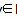Z；②任意m，n∈N*，有f(m)f(n)＝f(mn)＋f(m＋n－1)．
A∩B}．若A＝{x|y＝
}，B＝{y|y＝3x}，则A×B＝________．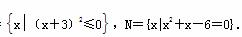
(1) 求(∁IM)∩N；