题目内容

椭圆C1：
x2
a2
+
y2
b2
=1(a＞b＞0)在第一象限部分的一点P，以P点横坐标作为长轴长，纵坐标作为短轴长作椭圆C2，如果C2的离心率等于C1的离心率，则P点坐标为
 
．
分析：先假设P点坐标，进而可得到椭圆C2的长轴和短轴与P点坐标的关系，然后表示出C1与C2的离心率，根据其离心率相等可得到C1与C2的长轴与短轴之间的关系，得到P点横纵坐标之间的关系，然后代入到椭圆中可得到P点的坐标．
解答：解：设p（x，y） 2a'=x  2b'=y
C1：e1=
1- (
b
a
)2
     C2：e2=
1-(
b′
a′
)2

∵e1=e2
∴
1- (
b
a
)2
=
1-(
b′
a′
)2

∴
b
a
 =
b′
a′
=
y
x

∴y=
bx
a
 
∴将y代入椭圆
x2
a2
+
y2
b2
=1 得x=
2
a
2

∴y=
2
b
a

故P点的坐标为：(
2
2
a，
2
2
b)
故答案为：(
2
2
a，
2
2
b)．
点评：本题主要考查椭圆的基本性质--离心率和半长轴、半短轴之间的关系．椭圆的基本性质是椭圆的基础，一般高考对椭圆的考查都是围绕着椭圆的性质进行展开的，故要对椭圆的基本性质熟练掌握．
练习册系列答案
相关题目
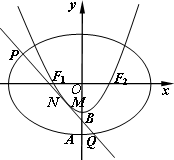精英家教网设椭圆C1：
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右焦点分别是F1、F2，下顶点为A，线段OA的中点为B（O为坐标原点），如图．若抛物线C2：y=x2-1与y轴的交点为B，且经过F1，F2点．
（Ⅰ）求椭圆C1的方程；
（Ⅱ）设M（0，-
4
5
），N为抛物线C2上的一动点，过点N作抛物线C2的切线交椭圆C1于P、Q两点，求△MPQ面积的最大值．
已知椭圆C1：
x2
a2
+
y2
b2
=1(a＞b＞0)的右焦点F2与抛物线C2：y2=4x的焦点重合，椭圆C1与抛物线C2在第一象限的交点为P，|PF2|=
5
3
，求椭圆C1的方程．
（2013•三门峡模拟）已知椭圆C1：
x2
a2
+
y2
b2
=1（a＞b＞0）的长轴长为4，离心率为
1
2
，F1、F2分别为其左右焦点．一动圆过点F2，且与直线x=-1相切．
（Ⅰ）（ⅰ）求椭圆C1的方程； （ⅱ）求动圆圆心C轨迹的方程；
（Ⅱ）在曲线上C有两点M、N，椭圆C1上有两点P、Q，满足MF2与
NF2
共线，
PF2
与
QF2
共线，且
PF2
•
MF2
=0，求四边形PMQN面积的最小值．
已知椭圆C1：
x2
A2
+
y2
B2
=1(A＞B＞0)和双曲线C2：
x2
a2
-
y2
b2
=1(a＞0，b＞0)有相同的焦点F1、F2，2c是它们的共同焦距，且它们的离心率互为倒数，P是它们在第一象限的交点，当cos∠F1PF2=60°时，下列结论中正确的是（　　）
（2013•汕头一模）已知椭圆C1：
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右焦点分别为F1、F2，右顶点为A，离心率e=
1
2

（1）设抛物线C2：y2=4x的准线与x轴交于F1，求椭圆的方程；
（2）设已知双曲线C3以椭圆C1的焦点为顶点，顶点为焦点，b是双曲线C3在第一象限上任意-点，问是否存在常数λ（λ＞0），使∠BAF1=λ∠BF1A恒成立？若存在，求出λ的值；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网