题目内容

已知数列{an}中，an+1=an+d2(d∈R),且a2、a5是方程x2-12x+27=0的两根，数列{bn}的前n项和为Sn,且Sn=1-bn(n∈N*).

(1)分别求出数列{an}、{bn}的通项；

(2)设cn=an·bn，试比较cn+1与cn的大小（n∈N*）.

解：(1)由a2、a5是方程x2-12x+27=0的两根与an+1=an+d2≥an，?

得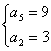3d2=9-3d2=2.?

∴等差数列{an}的公差为2，首项为1，an=1+(n-1)·2=2n-1.                              ?

又在数列{bn}中，Sn=1-bn,可得b1=.?

当n≥2时，bn=Sn-Sn-1=(1-bn)-(1-bn-1)bn=bn-1.?

所以数列{bn}是等比数列，b1=,公比为.?

bn=·()n-1=(n∈N*).                                                                                ?

(2)由cn=an·bn=得cn+1=.?

∵cn+1-cn==≤0,?

∴当n=1时，cn+1=cn;当n≥2时，cn+1＜cn.

练习册系列答案
相关题目
已知数列{an}中，a1=1，an+1-an=
1
3n+1
(n∈N*)，则
lim
n→∞
an=
 
．
已知数列{an}中，a1=1，an+1=
an
1+2an
，则{an}的通项公式an=
1
2n-1
1
2n-1
．
已知数列{an}中，a1=1，a1+2a2+3a3+…+nan=
n+1
2
an+1(n∈N*)．
（1）求数列{an}的通项公式；
（2）求数列{
2n
an
}的前n项和Tn．
已知数列{an}中，a1=
1
2
，Sn为数列的前n项和，且Sn与
1
an
的一个等比中项为n(n∈N*），则
lim
n→∞
Sn=
1
1
．
已知数列{an}中，a1=1，2nan+1=（n+1）an，则数列{an}的通项公式为（　　）
A、
n
2n
B、
n
2n-1
C、
n
2n-1
D、
n+1
2n

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网