题目内容
数列{an}满足:对任意的正整数m,n;s,t,若m+n=s+t,则 ,且
,且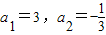 .
.(1)求证:
 ;
;(2)求数列{an}的通项公式;
(3)记cn=a2n-a2n+1(n∈N*),求证:
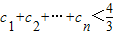 .
.
【答案】分析:(1)由于 ,所以条件可化为
,所以条件可化为 .故可得证.
.故可得证.
(2)将(1)式结论与条件相除得 ,令
,令 ,则:bmbn=bsbt由于1+n=2+(n-1),从而有b1bn=b2bn-1,可证数列为等比数列,从而求出数列的通项公式;
,则:bmbn=bsbt由于1+n=2+(n-1),从而有b1bn=b2bn-1,可证数列为等比数列,从而求出数列的通项公式;
(3)先证明 ,利用等比数列的求和公式求和,再进行放缩即可.
,利用等比数列的求和公式求和,再进行放缩即可.
解答:证明:(1)由 ①,
①,
得 ,
,
即 ②…(4分)
②…(4分)
(2)由②÷①得: ,
,
令 ,则:bmbn=bsbt由于1+n=2+(n-1),所以:b1bn=b2bn-1,所以:
,则:bmbn=bsbt由于1+n=2+(n-1),所以:b1bn=b2bn-1,所以: ,即:bn=-4bn-1(n≥2),所以:bn=b1(-4)n-1=
,即:bn=-4bn-1(n≥2),所以:bn=b1(-4)n-1= ,所以
,所以 (n∈N*)…(8分)
(n∈N*)…(8分)
(3)cn=a2n-a2n+1= =
=
所以 …(12分)
…(12分)
点评:本题的关键是挖掘结论与条件之间的联系,有一定的技巧性,综合性强.
 ,所以条件可化为
,所以条件可化为 .故可得证.
.故可得证.(2)将(1)式结论与条件相除得
 ,令
,令 ,则:bmbn=bsbt由于1+n=2+(n-1),从而有b1bn=b2bn-1,可证数列为等比数列,从而求出数列的通项公式;
,则:bmbn=bsbt由于1+n=2+(n-1),从而有b1bn=b2bn-1,可证数列为等比数列,从而求出数列的通项公式;(3)先证明
 ,利用等比数列的求和公式求和,再进行放缩即可.
,利用等比数列的求和公式求和,再进行放缩即可.解答:证明:(1)由
 ①,
①,得
 ,
,即
 ②…(4分)
②…(4分)(2)由②÷①得:
 ,
,令
 ,则:bmbn=bsbt由于1+n=2+(n-1),所以:b1bn=b2bn-1,所以:
,则:bmbn=bsbt由于1+n=2+(n-1),所以:b1bn=b2bn-1,所以: ,即:bn=-4bn-1(n≥2),所以:bn=b1(-4)n-1=
,即:bn=-4bn-1(n≥2),所以:bn=b1(-4)n-1= ,所以
,所以 (n∈N*)…(8分)
(n∈N*)…(8分)(3)cn=a2n-a2n+1=
 =
=
所以
 …(12分)
…(12分)点评:本题的关键是挖掘结论与条件之间的联系,有一定的技巧性,综合性强.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目