题目内容
已知不等式 对于一切大于1的自然数n都成立.
对于一切大于1的自然数n都成立.求证:实数a的取值范围是
 .
.
【答案】分析:先设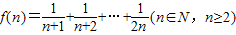 ,利用单调性的定义证得f(n)是关于n(n∈N,n≥2)的递增函数,从而有
,利用单调性的定义证得f(n)是关于n(n∈N,n≥2)的递增函数,从而有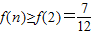 .要使原不等式成立,只需
.要使原不等式成立,只需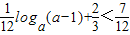 ,解此不等式即得.
,解此不等式即得.
解答:证明:设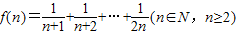 ,
,
∴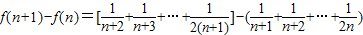
=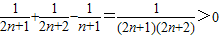 ,
,
∴f(n)是关于n(n∈N,n≥2)的递增函数,
∴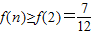 .
.
要使原不等式成立,只需: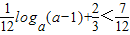 ,
,
即loga(a-1)<-1,
从而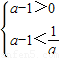 ,⇒
,⇒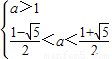 .
.
∴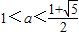 .
.
点评:本小题主要考查函数单调性的应用、不等式的证明、进行简单的演绎推理、不等式的证明等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.
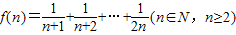 ,利用单调性的定义证得f(n)是关于n(n∈N,n≥2)的递增函数,从而有
,利用单调性的定义证得f(n)是关于n(n∈N,n≥2)的递增函数,从而有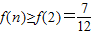 .要使原不等式成立,只需
.要使原不等式成立,只需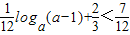 ,解此不等式即得.
,解此不等式即得.解答:证明:设
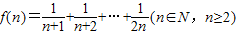 ,
,∴
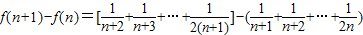
=
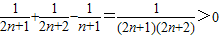 ,
,∴f(n)是关于n(n∈N,n≥2)的递增函数,
∴
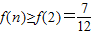 .
.要使原不等式成立,只需:
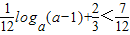 ,
,即loga(a-1)<-1,
从而
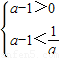 ,⇒
,⇒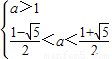 .
.∴
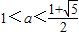 .
.点评:本小题主要考查函数单调性的应用、不等式的证明、进行简单的演绎推理、不等式的证明等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
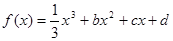 ,设曲线
,设曲线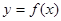 在与
在与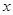 轴交点处的切线为
轴交点处的切线为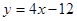 ,
,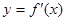 为
为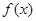 的导函数,满足
的导函数,满足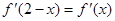 .
.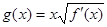 ,
,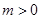 ,求函数
,求函数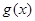 在
在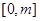 上的最大值;
上的最大值;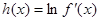 ,若对于一切
,若对于一切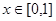 ,不等式
,不等式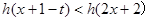 恒成立,求实数
恒成立,求实数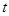 的取值范围.
的取值范围.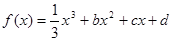 ,设曲线
,设曲线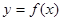 在与
在与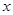 轴交点处的切线为
轴交点处的切线为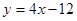 ,
,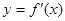 为
为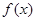 的导函数,满足
的导函数,满足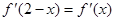 .
.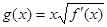 ,
,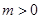 ,求函数
,求函数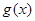 在
在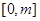 上的最大值;
上的最大值;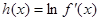 ,若对于一切
,若对于一切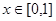 ,不等式
,不等式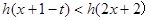 恒成立,求实数
恒成立,求实数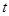 的取值范围.
的取值范围.