题目内容
已知函数 的定义域为
的定义域为 ,
,
(1)求 ;
;
(2)若 ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围.
【答案】
(1)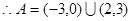 ;(2)
;(2)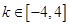 .
.
【解析】
试题分析:(1)求函数的定义域问题,涉及对数其真数应大于0,分母应不为0,二次根式的被开方数式应大于或等于0,注意考虑问题应全面,不逆漏.本题函数由意义需要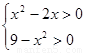 ,接不等是组记得元函数的定义域;(2)对集合
,接不等是组记得元函数的定义域;(2)对集合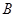 ,解方程
,解方程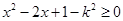 需要对
需要对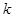 进行分类讨论.在由
进行分类讨论.在由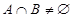 求出
求出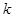 的取值范围.
的取值范围.
试题解析:(1)由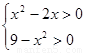 ,解得
,解得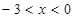 或
或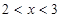 ,
,
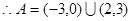 .
.
(2)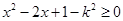 ,
,
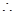 当
当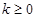 时,
时,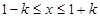 ,
,
当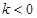 时,
时,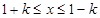 ,
,
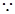
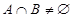 ,
,
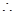
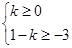 或
或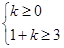 或解
或解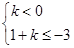 或
或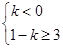 ,
,
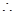
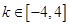
考点:函数的定义域,交集的概念,一元二次不等式的解法.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
已知函数 的定义域为
的定义域为 ,部分对应值如下表。
,部分对应值如下表。 的导函数
的导函数 的图像如图所示。
的图像如图所示。
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|

下列关于函数 的命题:
的命题:
①函数 在
在 上是减函数;②如果当
上是减函数;②如果当 时,
时, 最大值是
最大值是 ,那么
,那么 的最大值为
的最大值为 ;③函数
;③函数 有
有 个零点,则
个零点,则 ;④已知
;④已知 是
是 的一个单调递减区间,则
的一个单调递减区间,则 的最大值为
的最大值为 。
。
其中真命题的个数是( )
A、4个 B、3个 C、2个 D、1个
 的定义域为
的定义域为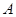 ,
,  ,且
,且 的真子集,求实数
的真子集,求实数 的取值范围.
的取值范围.




 的定义域为
的定义域为 ,且
,且 ,
, 为
为 ,
, 满足
满足 ,则
,则 的取值范围是
的取值范围是
 B.
B. C.
C. D.
D.