题目内容
 如图,已知△ABC周长为1,连接△ABC三边的中点构成第二个三角形,再连接第二个对角线三边中点构成第三个三角形,依此类推,第2003个三角形周长为
如图,已知△ABC周长为1,连接△ABC三边的中点构成第二个三角形,再连接第二个对角线三边中点构成第三个三角形,依此类推,第2003个三角形周长为
- A.

- B.

- C.

- D.

C
分析:根据题意,列出前几个三角形的周长,发现从第二项起,每个三角形的周长等于前一个三角形周长的一半,由此进行归纳即可得到第2003个三角形的周长.
解答:根据题意,设第k个三角形的周长记为ak,(k=1、2、3、…)
∵△ABC周长为1,∴a1=1
∵第二个三角形的三个顶点分别为三角形ABC三边的中点
∴第二个三角形的周长为a2= a1=
a1=
依此类推,第三个三角形的周长为a3= a2=
a2= ,…第k个三角形的周长为ak=
,…第k个三角形的周长为ak= ,…
,…
∴第2003个三角形周长为a2003= .
.
故选C
点评:本题以三角形的周长规律为载体,考查了归纳推理的一般方法和等比数列的通项公式的知识,属于基础题.
分析:根据题意,列出前几个三角形的周长,发现从第二项起,每个三角形的周长等于前一个三角形周长的一半,由此进行归纳即可得到第2003个三角形的周长.
解答:根据题意,设第k个三角形的周长记为ak,(k=1、2、3、…)
∵△ABC周长为1,∴a1=1
∵第二个三角形的三个顶点分别为三角形ABC三边的中点
∴第二个三角形的周长为a2=
 a1=
a1=
依此类推,第三个三角形的周长为a3=
 a2=
a2= ,…第k个三角形的周长为ak=
,…第k个三角形的周长为ak= ,…
,…∴第2003个三角形周长为a2003=
 .
.故选C
点评:本题以三角形的周长规律为载体,考查了归纳推理的一般方法和等比数列的通项公式的知识,属于基础题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
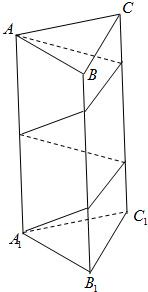 14、如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为8,一质点自A点出发,沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为
14、如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为8,一质点自A点出发,沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为 如图,已知正三棱柱ABC-A1B1C1的底面边长为2cm,高位5cm,一质点自A点出发,沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为
如图,已知正三棱柱ABC-A1B1C1的底面边长为2cm,高位5cm,一质点自A点出发,沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为 如图,已知梯形ABCD中,AD∥BC,∠ABC=90°,AD=a,BC=2a,∠DCB=60°,在平面ABCD内,过C作l⊥CB,以l为轴将梯形ABCD旋转一周,求所得旋转体的表面积及体积.
如图,已知梯形ABCD中,AD∥BC,∠ABC=90°,AD=a,BC=2a,∠DCB=60°,在平面ABCD内,过C作l⊥CB,以l为轴将梯形ABCD旋转一周,求所得旋转体的表面积及体积. (2012•蓝山县模拟)如图,已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,F为
(2012•蓝山县模拟)如图,已知BC是半径为1的半圆O的直径,A是半圆周上不同于B,C的点,F为
 (2012•徐汇区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D是AB的中点.
(2012•徐汇区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D是AB的中点.