题目内容
(本小题满分14分) 已知在单位圆x²+y²=1上任取一点M,作MN⊥x轴,垂足为N, 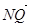 = 2
= 2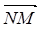 .
.
(Ⅰ)求动点Q的轨迹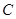 的方程;
的方程;
(Ⅱ)设点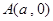 ,点
,点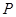 为曲线
为曲线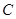 上任一点,求点
上任一点,求点 到点
到点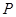 距离的最大值
距离的最大值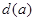 ;
;
(Ⅲ)在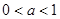 的条件下,设△
的条件下,设△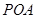 的面积为
的面积为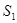 (
(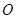 是坐标原点,
是坐标原点,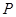 是曲线
是曲线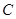 上横坐标为
上横坐标为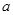 的点),以
的点),以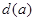 为边长的正方形的面积为
为边长的正方形的面积为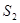 .若正数
.若正数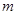 满足
满足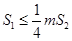 ,问
,问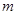 是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.
是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.
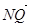 = 2
= 2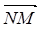 .
.(Ⅰ)求动点Q的轨迹
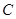 的方程;
的方程;(Ⅱ)设点
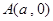 ,点
,点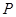 为曲线
为曲线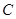 上任一点,求点
上任一点,求点 到点
到点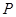 距离的最大值
距离的最大值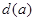 ;
;(Ⅲ)在
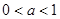 的条件下,设△
的条件下,设△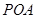 的面积为
的面积为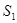 (
(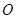 是坐标原点,
是坐标原点,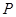 是曲线
是曲线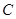 上横坐标为
上横坐标为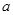 的点),以
的点),以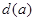 为边长的正方形的面积为
为边长的正方形的面积为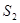 .若正数
.若正数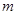 满足
满足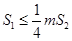 ,问
,问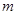 是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.
是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.(1)
(2) 时,
时,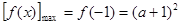 ;
;
 时,
时, ;
;
 时,,
时,, .所以,
.所以,
(3)

(2)
 时,
时,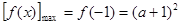 ;
; 时,
时, ;
; 时,,
时,, .所以,
.所以,
(3)

试题分析:解:(Ⅰ)设点Q的坐标为(x,y),M(x0,y0),则N(x0,0)
∴
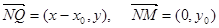
∵
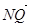 =
=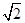
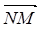
∴
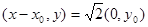
∵
 ∴
∴
∵点M(x0,y0)在单位圆x2 + y2 = 1上
∴

所以动点Q的轨迹C的方程为
 .........................4分
.........................4分(Ⅱ)设
 ,则
,则
 ,令
,令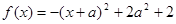 ,
, ,所以,
,所以,当
 ,即
,即 时
时 在
在 上是减函数,
上是减函数,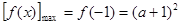 ;
;当
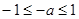 ,即
,即 时,
时, 在
在 上是增函数,在
上是增函数,在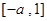 上是减函数,则
上是减函数,则 ;
;当
 ,即
,即 时,
时, 在
在 上是增函数,
上是增函数, .
.所以,
 . 9分
. 9分(Ⅲ)当
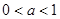 时,
时, ,于是
,于是 ,
, ,
,若正数
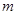 满足条件,则
满足条件,则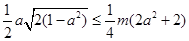 ,即
,即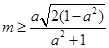 ,
,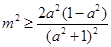 ,令
,令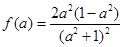 ,设
,设 ,则
,则 ,
,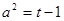 ,于是
,于是 ,
,所以,当
 ,即
,即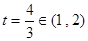 时,
时, ,
,即
 ,
, .所以,
.所以,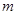 存在最小值
存在最小值 . 14分
. 14分点评:解决的关键是利用向量法坐标法得到轨迹方程,同时能利用点到直线的距离得到最值,属于基础题。

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 中,
中, ,则
,则 .
.
 ,则
,则 的夹角等于( )
的夹角等于( )



 中,
中, ,
, ,
,
 ,则
,则

 ,其中向量
,其中向量 ,
, .
.  )的值及f( x)的最大值。
)的值及f( x)的最大值。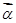 、
、 、
、 满足
满足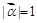 ,
,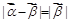 ,
, .若对每一确定的
.若对每一确定的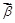 ,
, 的最大值和最小值分别为
的最大值和最小值分别为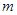 、
、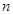 ,则对任意
,则对任意 的最小值是 ( )
的最小值是 ( )
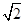
 中,
中, ,点
,点 分别是
分别是
 边上的动点,且
边上的动点,且 ,则
,则 的取值范围是 .
的取值范围是 . =2
=2 ,
, ·(
·( +
+ )等于( )
)等于( )

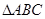 中,
中,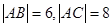 ,
,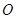 为
为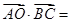 ________.
________.