题目内容
5.已知△ABC为直角三角形,AB是斜边,三个顶点在平面α的同侧,△ABC在平面α内的正投影为正△A′B′C′,且AA′=3,CC′=4,BB′=5,则△ABC的面积是$\frac{3}{2}$.分析 设正△A′B′C′的棱长为a,由勾股定理可得AC2=a2+1,BC2=a2+1,AB2=a2+4,AB2=AC2+BC2,求出AC,BC,代入三角形面积公式可得答案.
解答 解:已知中如下图所示: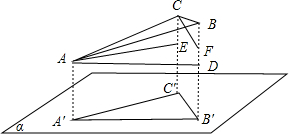
设正△A′B′C′的棱长为a,
∵AA′=3,CC′=4,BB′=5,
过A向BB′,CC′引垂线,垂足分别为D,E,
过C向BB′引垂线,垂足为F,
则AD=AE=CF=a,CE=BF=1,BD=2,
故AC2=a2+1,BC2=a2+1,AB2=a2+4,
由△ABC为直角三角形,AB是斜边,
故AB2=AC2+BC2,即a2+4=2(a2+1),
解得:a2=2,
故AC=BC=$\sqrt{3}$,
故△ABC的面积S=$\frac{1}{2}AC•BC$=$\frac{3}{2}$,
故答案为:$\frac{3}{2}$
点评 本题考查的知识点是平行投影,其中正确理解平行投影的定义,进而画出满足条件的图形是解答的关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
15.“a>b,c>0”是“ac>bc”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.直线l 交椭圆$\frac{x^2}{8}+\frac{y^2}{4}$=1于M、N两点,椭圆的上顶点为B点,若△BMN的重心恰好落在椭圆的右焦点上,则直线l的方程是( )
| A. | 2x-3y-9=0 | B. | 3x-2y-11=0 | C. | 3x+2y-7=0 | D. | x-y-5=0 |
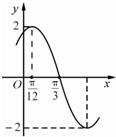 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)图象的一部分.
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)图象的一部分.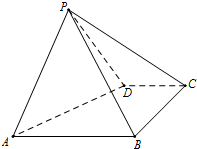 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形. 如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{2}$AD,PA⊥底面ABCD,过BC的平面交PD于M,交PA于N(M与D不重合).
如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{2}$AD,PA⊥底面ABCD,过BC的平面交PD于M,交PA于N(M与D不重合).