题目内容
如图已知椭圆的中点在原点,焦点在x轴上,长轴是短轴的2倍且过点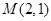 ,平行于
,平行于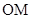 的直线
的直线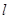 在y轴的截距为
在y轴的截距为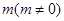 ,且交椭圆与
,且交椭圆与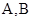 两点,
两点,
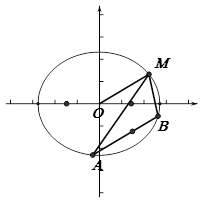
(1)求椭圆的方程;(2)求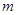 的取值范围;(3)求证:直线
的取值范围;(3)求证:直线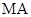 、
、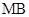 与x轴围成一个等腰三角形,说明理由.
与x轴围成一个等腰三角形,说明理由.
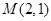 ,平行于
,平行于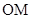 的直线
的直线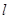 在y轴的截距为
在y轴的截距为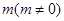 ,且交椭圆与
,且交椭圆与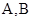 两点,
两点,
(1)求椭圆的方程;(2)求
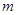 的取值范围;(3)求证:直线
的取值范围;(3)求证:直线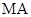 、
、 与x轴围成一个等腰三角形,说明理由.
与x轴围成一个等腰三角形,说明理由.(1)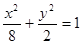 ;(2)
;(2)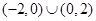 ;(3)详见解析
;(3)详见解析
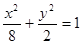 ;(2)
;(2)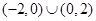 ;(3)详见解析
;(3)详见解析试题分析:直线和圆锥曲线位置关系问题,一般要将直线方程和圆锥曲线方程联立,同时要注意其隐含条件(
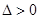 ),得关于某一个未知数的一元二次方程,利用韦达定理建立参数的等量关系或者不等关系,从而确定参数的值或者取值范围,(1)由椭圆焦点在
),得关于某一个未知数的一元二次方程,利用韦达定理建立参数的等量关系或者不等关系,从而确定参数的值或者取值范围,(1)由椭圆焦点在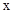 轴,先设椭圆标准方程为
轴,先设椭圆标准方程为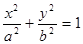
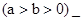 ,由已知得关于
,由已知得关于 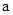 ,
,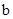 的方程组,解
的方程组,解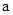 ,
,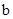 ;(2)注意条件“平行于
;(2)注意条件“平行于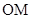 的直线
的直线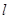 交椭圆与
交椭圆与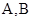 两点”,设直线方程为y=
两点”,设直线方程为y=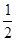 x+m,与椭圆联立,得关于
x+m,与椭圆联立,得关于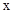 的一元二次方程,
的一元二次方程,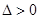 ,得
,得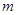 的取值范围(注意
的取值范围(注意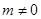 );(3)只需证明斜率互为相反数先设
);(3)只需证明斜率互为相反数先设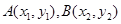 ,则
,则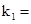
 ,
,
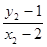 ,结合韦达定理证明
,结合韦达定理证明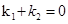 ;
; 试题解析:(1)设椭圆方程为
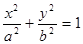 (a>b>0)
(a>b>0)则
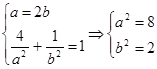 ∴椭圆方程
∴椭圆方程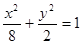 ;
;(2)∵直线
 ∥DM且在y轴上的截距为m,∴y=
∥DM且在y轴上的截距为m,∴y=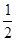 x+m
x+m由
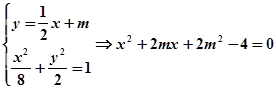
∵
 与椭圆交于A、B两点∴△=(2m)2-4(2m2-4)>0
与椭圆交于A、B两点∴△=(2m)2-4(2m2-4)>0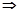 -2<m<2(m≠0);
-2<m<2(m≠0);(3)设直线MA、MB斜率分别为k1,k2,则只要证:k1+k2=0
设A(x1,y1),B(x2,y2),则k1=
 ,k2=
,k2=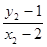
由x2+2mx+2m2-4=0得x1+x2=-2m,x1x2=2m2-4
而k1+k2=
 +
+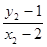 =
= (*)
(*)又y1=
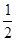 x1+m y2=
x1+m y2=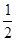 x2+m
x2+m∴(*)分子=(
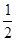 x1+m-1)(x2-2)+(
x1+m-1)(x2-2)+(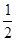 x2+m-1)(x1-2)
x2+m-1)(x1-2)=x1x2+(m-2)(x1+x2)-4(m-1)
=2m2-4+(m-2)(-m)-4(m-1)=0
∴k1+k2=0,证之.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 ,若焦点在
,若焦点在 轴上的椭圆
轴上的椭圆 过点
过点 ,且其长轴长等于圆
,且其长轴长等于圆 的直径.
的直径. 作两条互相垂直的直线
作两条互相垂直的直线 与
与 ,
, 、
、 两点,
两点, ,设直线
,设直线 ,求弦
,求弦 长;
长; 面积的最大值.
面积的最大值.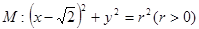 ,若椭圆
,若椭圆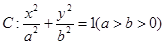 的右顶点为圆
的右顶点为圆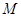 的圆心,离心率为
的圆心,离心率为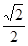 .
.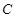 的方程;
的方程;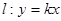 ,使得直线
,使得直线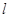 与椭圆
与椭圆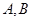 两点,与圆
两点,与圆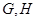 两点,点
两点,点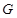 在线段
在线段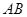 上,且
上,且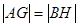 ,求圆
,求圆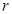 的取值范围.
的取值范围. 中,点
中,点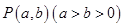 为动点,
为动点, 、
、 分别为椭圆
分别为椭圆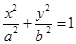 的左、右焦点.已知
的左、右焦点.已知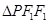 为等腰三角形.
为等腰三角形.
 ;
;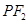 与椭圆相交于
与椭圆相交于 、
、 两点,
两点, 是直线
是直线 ,求点
,求点 )。
)。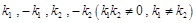 为斜率的直线分别交椭圆C于A,B,M,N,求证:
为斜率的直线分别交椭圆C于A,B,M,N,求证:  使得
使得
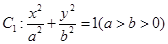 的离心率为
的离心率为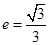 ,直线
,直线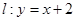 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆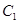 的短半轴长为半径的圆
的短半轴长为半径的圆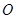 相切.
相切.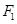 ,右焦点为
,右焦点为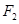 ,直线
,直线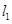 过点
过点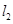 垂直于
垂直于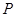 ,线段
,线段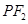 的垂直平分线交
的垂直平分线交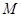 ,求点
,求点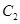 的方程;
的方程;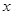 轴交于点
轴交于点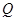 ,不同的两点
,不同的两点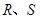 在
在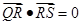 ,求
,求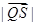 的取值范围.
的取值范围.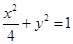 的左焦点作互相垂直的两条直线,分别交椭圆于
的左焦点作互相垂直的两条直线,分别交椭圆于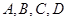 四点,则四边形
四点,则四边形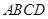 面积的最大值与最小值之差为( )
面积的最大值与最小值之差为( )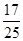
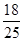
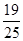
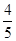
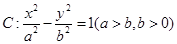 的左、右焦点,过左焦点F1的直线
的左、右焦点,过左焦点F1的直线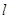 与双曲线C的左、右两支分别交于A,B两点,若
与双曲线C的左、右两支分别交于A,B两点,若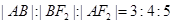 ,则双曲线的离心率是( )
,则双曲线的离心率是( )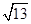
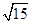
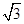
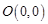 ,
,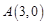 ,动点
,动点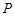 到定点
到定点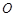 距离与到定点
距离与到定点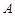 的距离的比值是
的距离的比值是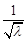 .
.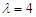 时,记动点
时,记动点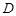 .
.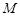 是圆
是圆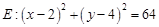 上任意一点,过
上任意一点,过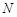 ,求
,求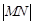 的取值范围;
的取值范围;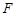 ,
,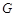 是曲线
是曲线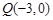 ,有
,有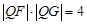 .试问无论
.试问无论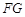 能恒和一个定圆相切吗?若能,求出这个定圆的方程;若不能,请说明理由.
能恒和一个定圆相切吗?若能,求出这个定圆的方程;若不能,请说明理由.