题目内容
已知椭圆 的下顶点为A,点B是椭圆上的任意的一点,点C、D是直线x-y-4=0上的两点(C在D的下方),则
的下顶点为A,点B是椭圆上的任意的一点,点C、D是直线x-y-4=0上的两点(C在D的下方),则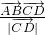 的最大值是
的最大值是
- A.
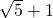
- B.
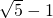
- C.
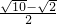
- D.
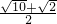
D
分析:由于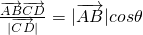 表示向量
表示向量 在直线CD上的投影的长度,如图,设与直线x-y-4=0上垂直的直线方程为:y=-x+b,代入椭圆的方程得到关于x 的二次主程,由△=0得:b=
在直线CD上的投影的长度,如图,设与直线x-y-4=0上垂直的直线方程为:y=-x+b,代入椭圆的方程得到关于x 的二次主程,由△=0得:b= ,结合图形得
,结合图形得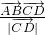 的最大值是点A到此切线的距离,利用点到直线的距离公式求解即得.
的最大值是点A到此切线的距离,利用点到直线的距离公式求解即得.
解答: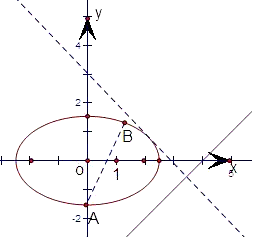 解:由于
解:由于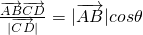 表示向量
表示向量 在直线CD上的投影的长度,如图,
在直线CD上的投影的长度,如图,
设与直线x-y-4=0上垂直的直线方程为:
y=-x+b,
代入椭圆的方程 得:
得: x2-2bx+b2-1=0,
x2-2bx+b2-1=0,
由△=0得:b= ,
,
结合图形得,图中椭圆的切线方程为:y=-x+ ,
,
则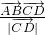 的最大值是点A到此切线的距离,即
的最大值是点A到此切线的距离,即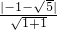 =
=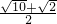 .
.
故选D.
点评:本小题主要考查椭圆的方程、直线与椭圆的位置关系等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
分析:由于
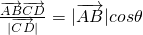 表示向量
表示向量 在直线CD上的投影的长度,如图,设与直线x-y-4=0上垂直的直线方程为:y=-x+b,代入椭圆的方程得到关于x 的二次主程,由△=0得:b=
在直线CD上的投影的长度,如图,设与直线x-y-4=0上垂直的直线方程为:y=-x+b,代入椭圆的方程得到关于x 的二次主程,由△=0得:b= ,结合图形得
,结合图形得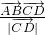 的最大值是点A到此切线的距离,利用点到直线的距离公式求解即得.
的最大值是点A到此切线的距离,利用点到直线的距离公式求解即得.解答:
 解:由于
解:由于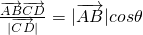 表示向量
表示向量 在直线CD上的投影的长度,如图,
在直线CD上的投影的长度,如图,设与直线x-y-4=0上垂直的直线方程为:
y=-x+b,
代入椭圆的方程
 得:
得: x2-2bx+b2-1=0,
x2-2bx+b2-1=0,由△=0得:b=
 ,
,结合图形得,图中椭圆的切线方程为:y=-x+
 ,
,则
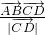 的最大值是点A到此切线的距离,即
的最大值是点A到此切线的距离,即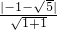 =
=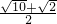 .
.故选D.
点评:本小题主要考查椭圆的方程、直线与椭圆的位置关系等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
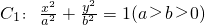 的上顶点为A(0,1),过C1的焦点且垂直长轴的弦长轴的弦长为1.
的上顶点为A(0,1),过C1的焦点且垂直长轴的弦长轴的弦长为1.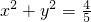 ,过该圆上任意一点作圆的切线l,试证明l和椭圆C1恒有两个交点A,B,且有
,过该圆上任意一点作圆的切线l,试证明l和椭圆C1恒有两个交点A,B,且有 ;
;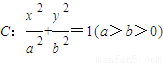 的左顶点为A,右焦点为F,且过点(1,
的左顶点为A,右焦点为F,且过点(1, ),椭圆C的焦点与曲线
),椭圆C的焦点与曲线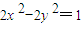 的焦点重合.
的焦点重合.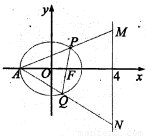
 的下顶点为A,点B是椭圆上的任意的一点,点C、D是直线x-y-4=0上的两点(C在D的下方),则
的下顶点为A,点B是椭圆上的任意的一点,点C、D是直线x-y-4=0上的两点(C在D的下方),则 的最大值是( )
的最大值是( )



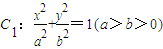 的上顶点为A(0,1),过C1的焦点且垂直长轴的弦长轴的弦长为1.
的上顶点为A(0,1),过C1的焦点且垂直长轴的弦长轴的弦长为1.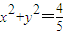 ,过该圆上任意一点作圆的切线l,试证明l和椭圆C1恒有两个交点A,B,且有
,过该圆上任意一点作圆的切线l,试证明l和椭圆C1恒有两个交点A,B,且有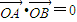 ;
;