题目内容
已知椭圆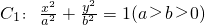 的上顶点为A(0,1),过C1的焦点且垂直长轴的弦长轴的弦长为1.
的上顶点为A(0,1),过C1的焦点且垂直长轴的弦长轴的弦长为1.
(1)求椭圆C1的方程;
(2)设圆O: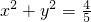 ,过该圆上任意一点作圆的切线l,试证明l和椭圆C1恒有两个交点A,B,且有
,过该圆上任意一点作圆的切线l,试证明l和椭圆C1恒有两个交点A,B,且有 ;
;
(3)在(2)的条件下求弦AB长度的取值范围.
解:依题意有 .
.
(1) .
.
(2)由 ,且半径
,且半径 ,所以圆O必在椭圆内部,
,所以圆O必在椭圆内部,
所以过该圆上任意一点作切线必与椭圆恒有两个交点.
设切点坐标为(x0,y0),A(x1,y1),B(x2,y2),
则切线方程为 (1),
(1),
又由(1)知 (2)
(2)
联立(1)(2)得: ,
, ,
,
又 ,
, ,
,
所以,欲证 ,即证:x1x2+y1y2=0,
,即证:x1x2+y1y2=0,
因为:
所以, 命题成立.
命题成立.
(3)设∠A=θ,则∠B=90°-θ, ,
, ,
,
则 ,
,
所以OA∈[1,2], ,所以
,所以 ,又θ为锐角,
,又θ为锐角,
所以 ,则有
,则有 ,所以
,所以 .
.
分析:(1)根据点A的坐标求得b,根据过C1的焦点且垂直长轴的弦长轴的弦长为1.求得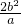 =1,进而求得a,则椭圆的方程可得.
=1,进而求得a,则椭圆的方程可得.
(2)根据椭圆方程和圆的半径小于1判断圆O必在椭圆内部设切点坐标为(x0,y0),A(x1,y1),B(x2,y2),进而可表示出切线方程,与椭圆方程联立消去y,根据韦达定理表示出x1+x2和x1x2,进而根据y1和y2的表达式,求得y1y2的表达式,进而代入x1x2+y1y2求得结果为0,进而判断出 .
.
(3)设∠A=θ,则∠B=90°-θ,可知OD的值,进而表示出BD和AD,进而表示出AB,确定OA的范围, 确定sinθ的范围,推断出tanθ的范围,进而确定AB的范围.
确定sinθ的范围,推断出tanθ的范围,进而确定AB的范围.
点评:本题主要考查了椭圆的应用.考查了学生综合分析问题和基本的运算能力.
 .
.(1)
 .
.(2)由
 ,且半径
,且半径 ,所以圆O必在椭圆内部,
,所以圆O必在椭圆内部,所以过该圆上任意一点作切线必与椭圆恒有两个交点.
设切点坐标为(x0,y0),A(x1,y1),B(x2,y2),
则切线方程为
 (1),
(1),又由(1)知
 (2)
(2)联立(1)(2)得:
 ,
, ,
,又
 ,
, ,
,所以,欲证
 ,即证:x1x2+y1y2=0,
,即证:x1x2+y1y2=0,因为:

所以,
 命题成立.
命题成立.(3)设∠A=θ,则∠B=90°-θ,
 ,
, ,
,则
 ,
,所以OA∈[1,2],
 ,所以
,所以 ,又θ为锐角,
,又θ为锐角,所以
 ,则有
,则有 ,所以
,所以 .
.分析:(1)根据点A的坐标求得b,根据过C1的焦点且垂直长轴的弦长轴的弦长为1.求得
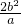 =1,进而求得a,则椭圆的方程可得.
=1,进而求得a,则椭圆的方程可得.(2)根据椭圆方程和圆的半径小于1判断圆O必在椭圆内部设切点坐标为(x0,y0),A(x1,y1),B(x2,y2),进而可表示出切线方程,与椭圆方程联立消去y,根据韦达定理表示出x1+x2和x1x2,进而根据y1和y2的表达式,求得y1y2的表达式,进而代入x1x2+y1y2求得结果为0,进而判断出
 .
.(3)设∠A=θ,则∠B=90°-θ,可知OD的值,进而表示出BD和AD,进而表示出AB,确定OA的范围,
 确定sinθ的范围,推断出tanθ的范围,进而确定AB的范围.
确定sinθ的范围,推断出tanθ的范围,进而确定AB的范围.点评:本题主要考查了椭圆的应用.考查了学生综合分析问题和基本的运算能力.

练习册系列答案
相关题目
 的上顶点为A,直线y=-4交椭圆E于点B,C(点B在点C的左侧),点P在椭圆E上.
的上顶点为A,直线y=-4交椭圆E于点B,C(点B在点C的左侧),点P在椭圆E上.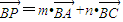 (m,n为实数),求m+n的最大值.
(m,n为实数),求m+n的最大值.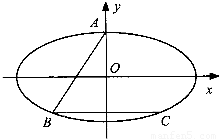
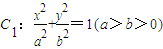 的上顶点为A(0,1),过C1的焦点且垂直长轴的弦长轴的弦长为1.
的上顶点为A(0,1),过C1的焦点且垂直长轴的弦长轴的弦长为1.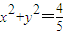 ,过该圆上任意一点作圆的切线l,试证明l和椭圆C1恒有两个交点A,B,且有
,过该圆上任意一点作圆的切线l,试证明l和椭圆C1恒有两个交点A,B,且有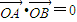 ;
;