题目内容
在△ABC中,BC=2,AC= ,AB=
,AB= .设
.设 .
.
(1)求 ;
;
(2)证明:A、P、C三点共线;
(3)当△ABP的面积为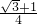 时,求λ的值.
时,求λ的值.
(1)解:∵△ABC中,BC=2,AC= ,AB=
,AB= ,
,
∴由余弦定理知:cosA= =
=
∴ =
= cosA=
cosA= ;
;
(2)证明:∵
∴ ,
,
∴ (λ>0),
(λ>0),
∵ 有公共点A
有公共点A
∴A、P、C三点共线.
(3)解:∵S△ABP= AB•AP•sinA=
AB•AP•sinA= (
( )•AP•
)•AP• =
=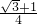 ,
,
∴AP= ,
,
∵AC= ,∴λ=
,∴λ= .
.
分析:(1)利用余弦定理,计算cosA,再利用向量的数量积公式,即可求得结论;
(2)利用向量共线定理,证明 即可;
即可;
(3)利用三角形的面积公式,计算AP,即可求λ的值.
点评:本题考查向量的综合运算,考查余弦定理的运用,考查三角形面积的计算,属于中档题.
 ,AB=
,AB= ,
,∴由余弦定理知:cosA=
 =
=
∴
 =
= cosA=
cosA= ;
;(2)证明:∵

∴
 ,
,∴
 (λ>0),
(λ>0),∵
 有公共点A
有公共点A∴A、P、C三点共线.
(3)解:∵S△ABP=
 AB•AP•sinA=
AB•AP•sinA= (
( )•AP•
)•AP• =
=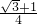 ,
,∴AP=
 ,
,∵AC=
 ,∴λ=
,∴λ= .
.分析:(1)利用余弦定理,计算cosA,再利用向量的数量积公式,即可求得结论;
(2)利用向量共线定理,证明
 即可;
即可;(3)利用三角形的面积公式,计算AP,即可求λ的值.
点评:本题考查向量的综合运算,考查余弦定理的运用,考查三角形面积的计算,属于中档题.

练习册系列答案
相关题目
在△ABC中,|BC|=2|AB|,∠ABC=120°,则以A,B为焦点且过点C的双曲线的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中,(
+
)•
=|
|2,
•
=3,|
|=2,则△ABC的面积是( )
| BC |
| BA |
| AC |
| AC |
| BA |
| BC |
| BC |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |