题目内容
（2013•朝阳区二模）若直线l与圆x2+（y+1）2=4相交于A，B两点，且线段AB的中点坐标是（1，-2），则直线l的方程为
x-y-3=0
x-y-3=0
．分析：设圆心为C，AB的中点为D，由直线和圆相交的性质可得，直线l⊥CD，求出直线l的斜率为
的值，再用点斜式求得直线l的方程．
| -1 |
| KCD |
解答：解：设圆C：x2+（y+1）2=4的圆心C（0，-1），弦AB的中点坐标是D（1，-2），
由直线和圆相交的性质可得 直线l⊥CD，∴直线l的斜率为
=
=1，
故直线l的方程为 y+2=x-1，即 x-y-3=0，
故答案为 x-y-3=0．
由直线和圆相交的性质可得 直线l⊥CD，∴直线l的斜率为
| -1 |
| KCD |
| -1 | ||
|
故直线l的方程为 y+2=x-1，即 x-y-3=0，
故答案为 x-y-3=0．
点评：本题主要考查直线和圆相交的性质，用点斜式求直线的方程，属于中档题．
练习册系列答案
相关题目
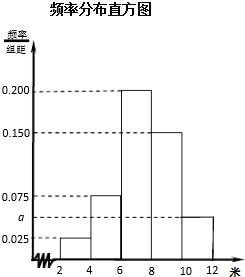（2013•朝阳区二模）为了解某市今年初二年级男生的身体素质状况，从该市初二年级男生中抽取了一部分学生进行“掷实心球”的项目测试．成绩低于6米为不合格，成绩在6至8米（含6米不含8米）的为及格，成绩在8米至12米（含8米和12米，假定该市初二学生掷实心球均不超过12米）为优秀．把获得的所有数据，分成[2，4），[4，6），[6，8），[8，10），[10，12]五组，画出的频率分布直方图如图所示．已知有4名学生的成绩在10米到12米之间．