题目内容
(2013•朝阳区二模)在△ABC中,角A,B,C所对的边分别为a,b,c,且f(A)=2cos
sin(π-
)+sin2
-cos2
.
(Ⅰ)求函数f(A)的最大值;
(Ⅱ)若f(A)=0,C=
,a=
,求b的值.
| A |
| 2 |
| A |
| 2 |
| A |
| 2 |
| A |
| 2 |
(Ⅰ)求函数f(A)的最大值;
(Ⅱ)若f(A)=0,C=
| 5π |
| 12 |
| 6 |
分析:(Ⅰ)利用三角恒等变换化简函数f(A)为
sin(A-
),根据0<A<π,利用正弦函数的定义域和值域求得f(A)取得最大值.
(Ⅱ)由题意知f(A)=
sin(A-
)=0,由此求得A的值,再根据C的值,求得B的值,利用正弦定理求出b的值.
| 2 |
| π |
| 4 |
(Ⅱ)由题意知f(A)=
| 2 |
| π |
| 4 |
解答:解:(Ⅰ)f(A)=2cos
sin
+sin2
-cos2
=sinA-cosA=
sin(A-
).
因为0<A<π,所以-
<A-
<
.
则所以当A-
=
,即A=
时,f(A)取得最大值,且最大值为
.…(7分)
(Ⅱ)由题意知f(A)=
sin(A-
)=0,所以sin(A-
)=0.
又知-
<A-
<
,所以A-
=0,则A=
.
因为C=
,所以A+B=
,则B=
.
由
=
得,b=
=
=3. …(13分)
| A |
| 2 |
| A |
| 2 |
| A |
| 2 |
| A |
| 2 |
| 2 |
| π |
| 4 |
因为0<A<π,所以-
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
则所以当A-
| π |
| 4 |
| π |
| 2 |
| 3π |
| 4 |
| 2 |
(Ⅱ)由题意知f(A)=
| 2 |
| π |
| 4 |
| π |
| 4 |
又知-
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| π |
| 4 |
因为C=
| 5π |
| 12 |
| 7π |
| 12 |
| π |
| 3 |
由
| a |
| sinA |
| b |
| sinB |
| asinB |
| sinA |
| ||||
sin
|
点评:本题主要考查三角恒等变换,正弦定理、正弦函数的定义域和值域,属于中档题.

练习册系列答案
相关题目
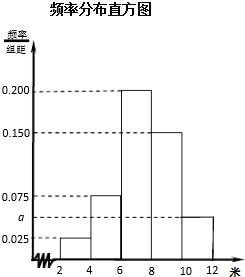 (2013•朝阳区二模)为了解某市今年初二年级男生的身体素质状况,从该市初二年级男生中抽取了一部分学生进行“掷实心球”的项目测试.成绩低于6米为不合格,成绩在6至8米(含6米不含8米)的为及格,成绩在8米至12米(含8米和12米,假定该市初二学生掷实心球均不超过12米)为优秀.把获得的所有数据,分成[2,4),[4,6),[6,8),[8,10),[10,12]五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.
(2013•朝阳区二模)为了解某市今年初二年级男生的身体素质状况,从该市初二年级男生中抽取了一部分学生进行“掷实心球”的项目测试.成绩低于6米为不合格,成绩在6至8米(含6米不含8米)的为及格,成绩在8米至12米(含8米和12米,假定该市初二学生掷实心球均不超过12米)为优秀.把获得的所有数据,分成[2,4),[4,6),[6,8),[8,10),[10,12]五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在10米到12米之间.