题目内容
12.正四面体ABCD中,棱AB与底面BCD所成角在余弦值是$\frac{\sqrt{3}}{3}$.分析 在正四面体ABCD中,过A作AH⊥平面BCD于点H,则H为底面正三角形BCD的外心,连接BH,则∠ABH=α,就是AB与平面BCD所成角,解直角三角形ABH即可.
解答 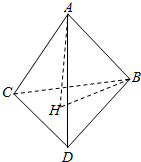 解:正四面体ABCD,高为AH,
解:正四面体ABCD,高为AH,
则H为底面正三角形BCD的外心,则∠ABH=α,就是AB与平面BCD所成角,
在Rt△ABH中,设棱长为a,
则BH=a×$\frac{\sqrt{3}}{2}$×$\frac{2}{3}$=$\frac{\sqrt{3}}{3}a$,AH=$\sqrt{{a}^{2}-({\frac{\sqrt{3}}{3}a)}^{2}}$=$\frac{\sqrt{6}}{3}a$,
∴cosα=$\frac{HB}{AB}$=$\frac{\frac{\sqrt{3}}{3}a}{a}$=$\frac{\sqrt{3}}{3}$.
故答案为:$\frac{\sqrt{3}}{3}$.
点评 考查直线和平面所成的角,关键是找到斜线在平面内的射影,把空间角转化为平面角求解,属中档题.

练习册系列答案
相关题目
3.已知tan(-α-$\frac{4}{3}$π)=-5,则tan($\frac{π}{3}$+α)的值为( )
| A. | 5 | B. | -5 | C. | ±5 | D. | 不确定 |
20.函数y=$\sqrt{{log}_{0.5}(4x-3)}$的定义域为A,全集为R,则∁RA为( )
| A. | ($\frac{3}{4}$,1] | B. | [$\frac{3}{4}$,1) | C. | (-∞,$\frac{3}{4}$]∪(1,+∞) | D. | (-∞,$\frac{3}{4}$]∪[1,+∞) |
7.已知直线l1:2x+ay=3和l2:(a+2)x-y=1直线互相垂直,则实数a的值为( )
| A. | -2 | B. | 2 | C. | -4 | D. | 4 |
1.设α,β是两个不同的平面,l,m是两条不同的直线,命题p:α∥β,l?α,m?β,则l∥m;命题q:l∥α,m⊥l,m?β,则β⊥α.下列命题为真命题的是( )
| A. | p或q | B. | p且q | C. | p或q | D. | p且q |
2.已知f(x)=$\sqrt{3}$sinx-cosx,f′(x)是f(x)的导函数,若f(x0)=$\frac{1}{2}$,则f′(2x0-$\frac{π}{6}$)=( )
| A. | -$\frac{7}{8}$ | B. | $\frac{7}{8}$ | C. | -$\frac{7}{4}$ | D. | $\frac{7}{4}$ |