题目内容

在△OAB中，M为OB的中点，N为AB的中点，ON，AM交于点P，若
AP
=m
OA
+n
OB
（m，n∈R），则n-m=
1
1
．
分析：将
OA
=
a
，
OB
=
b
看做一组基底，运用向量加法的三角形法则和已知的比例关系，将向量用这组基底表示，即可得唯一的m、n的值，进而作差得结果
解答：解：设
OA
=
a
，
OB
=
b

由
AP
=
AO
+
OP

=
AO
+
2
3
ON

=-
a
+
1
3
(
a
+
b
)
=-
2
3
a
+
1
3
b

∵
AP
=m
OA
+n
OB
=
AP
=m
a
+n
b

∴m=-
2
3
，n=
1
3

∴n-m=
1
3
+
2
3
=1
故答案为 1
点评：本题主要考查了平面向量的基本定理及其应用，向量加法的三角形法则等基础知识，数形结合的思想方法，运用向量加法的三角形法则和已知的比例关系，将向量用一组基底表示，是解决本题的关键
练习册系列答案
相关题目
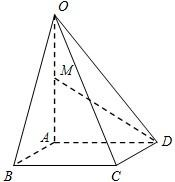精英家教网如图，在四棱锥O-ABCD中，底面ABCD是边长为1的菱形，∠ABC=
π4
，OA⊥底面ABCD，OA=2，M为OA的中点．
（Ⅰ）求异面直线AB与MD所成角的大小；
（Ⅱ）求平面OAB与平面OCD所成的二面角的余弦值．
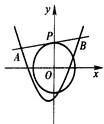精英家教网设点P（m，n）在圆x2+y2=2上，l是过点P的圆的切线，切线l与函数y=x2+x+k（k∈R）的图象交于A，B两点，点O是坐标原点．
（1）当k=-2，m=-1，n=-1时，判断△OAB的形状；
（2）△OAB是以AB为底的等腰三角形；
①试求出P点纵坐标n满足的等量关系；
②若将①中的等量关系右边化为零，左边关于n的代数式可表为（n+1）2（ax2+bx+c）的形式，且满足条件的等腰三角形有3个，求k的取值范围．

如图，在四棱锥O－ABCD中，底面ABCD是边长为1的菱形，∠ABC＝45°，OA⊥底面ABCD，OA＝2，M为OA的中点．

（1）求异面直线AB与MD所成角的大小；

（2）求平面OAB与平面OCD所成二面角的余弦值．

 
如图，在四棱锥O﹣ABCD中，底面ABCD是边长为1的菱形，，OA⊥底面ABCD，OA=2，M为OA的中点．
（Ⅰ）求异面直线AB与MD所成角的大小；
（Ⅱ）求平面OAB与平面OCD所成的二面角的余弦值．
如图，在四棱锥O-ABCD中，底面ABCD是边长为1的菱形，，OA⊥底面ABCD，OA=2，M为OA的中点．
（Ⅰ）求异面直线AB与MD所成角的大小；
（Ⅱ）求平面OAB与平面OCD所成的二面角的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网