题目内容
20.函数y=|sin($\frac{π}{6}$-2x)+sin2x|的最小正周期是$\frac{π}{2}$.分析 利用三角函数的恒等式化简函数y,并考虑绝对值对函数y周期的影响即可.
解答 解:∵函数y=|sin($\frac{π}{6}$-2x)+sin2x|
=|sin$\frac{π}{6}$cos2x-cos$\frac{π}{6}$sin2x+sin2x|
=|$\frac{1}{2}$cos2x+(1-$\frac{\sqrt{3}}{2}$)sin2x|
=$\sqrt{2-\sqrt{3}}$|sin(2x+θ)|,其中θ=arctan(2-$\sqrt{3}$);
∴函数y的最小正周期是
T=$\frac{1}{2}$×$\frac{2π}{ω}$=$\frac{1}{2}$×$\frac{2π}{2}$=$\frac{π}{2}$.
故答案为:$\frac{π}{2}$.
点评 本题考查了三角函数最小正周期的求法问题,解题时应先将函数化简为y=Asin(ωx+ρ)的形式,再求T,还应考虑绝对值对周期的影响,是基础题目.

练习册系列答案
相关题目
10.下列不等式在给定区间上不恒成立的是( )
| A. | (x+1)cosx<1,x∈(0,π) | B. | e${\;}^{{x}^{2}}$>1+x2,x∈(0,+∞) | ||
| C. | sinx+tanx>2x,x∈(0,$\frac{π}{2}$) | D. | lnx+ex>x$-\frac{1}{x}$+2,x∈(0,+∞) |
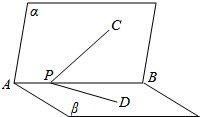 如图,平面α⊥平面β,平面α∩平面β=AB,P∈AB,C∈α,D∈β,且∠CPB=∠DPB=45°,则∠CPD=60°.
如图,平面α⊥平面β,平面α∩平面β=AB,P∈AB,C∈α,D∈β,且∠CPB=∠DPB=45°,则∠CPD=60°. 如图为一半径是3米的水轮,水轮圆心O距离水面2米,开始旋转时水轮上的点P在P0位置,P0距离水面3米,已知水轮每分钟旋转4圈,求点P到水面的距离y(米)与时间x(秒)的函数关系式.
如图为一半径是3米的水轮,水轮圆心O距离水面2米,开始旋转时水轮上的点P在P0位置,P0距离水面3米,已知水轮每分钟旋转4圈,求点P到水面的距离y(米)与时间x(秒)的函数关系式.