题目内容
如图所示,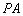 ⊥平面
⊥平面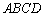 ,△
,△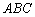 为等边三角形,
为等边三角形,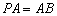 ,
, ⊥
⊥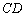 ,
,
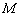 为
为 中点.
中点.
(I)证明: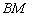 ∥平面
∥平面 ;
;
(II)若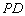 与平面
与平面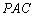 所成角的正切值 为
所成角的正切值 为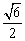 ,求二面角
,求二面角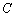 -
-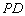 -
-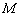 的正切值.
的正切值.

解:(Ⅰ)证明:因为M为等边△ABC的AC边的中点,所以BM⊥AC.
依题意CD⊥AC,且A、B、C、D四点共面,所以BM∥CD. …………2分
又因为BMË平面PCD,CDÌ平面PCD,所以BM∥平面PCD. …………5分
(Ⅱ)因为CD⊥AC,CD⊥PA,
所以CD⊥平面PAC,故PD与平面
PAC所成的角即为∠CPD.
……………5分
不妨设PA=AB=1,则PC=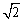 .
.
由于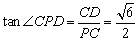 ,
,
所以CD=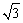 .……………8分
.……………8分
(方法一)
在等腰Rt△PAC中,过点M作ME⊥PC于点E,再在Rt△PCD中作EF⊥PD于点F.因为ME⊥PC,ME⊥CD,所以ME⊥平面PCD,可得ME⊥PD.
又EF⊥PD,所以∠EFM即为二面角C-PD-M的平面角.
易知PE=3EC,ME=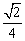 ,EF=
,EF= ,
,
 所以tan∠EFM=
所以tan∠EFM= ,
,
即二面角C-PD-M的正切值是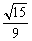 .
.
……………12分
(方法二)
以A点为坐标原点,AC为x轴,建立
如图所示的空间直角坐标系A﹣xyz.
则P(0,0,1),
M(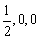 ),C(1,0,0),D
),C(1,0,0),D .
.
则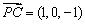 ,
,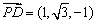 ,
,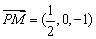 .
.
若设 和
和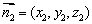 分别是平面PCD和平面PMD的法向量,则
分别是平面PCD和平面PMD的法向量,则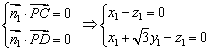 ,可取
,可取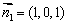 .
.
由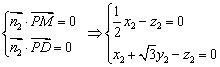 ,可取
,可取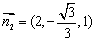 .
.
所以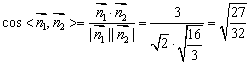 ,
,

练习册系列答案
相关题目
 如图,在四棱锥
如图,在四棱锥 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, 是
是 的中点.
的中点. 的体积;
的体积; 和
和 所成的角(结果
所成的角(结果 轴的椭圆
轴的椭圆 ,则它的离心率的取值范围为 .
,则它的离心率的取值范围为 .  为坐标原点,
为坐标原点, 为抛物线
为抛物线 的焦点,
的焦点, 为
为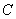 上一点,若
上一点,若 ,
, 的面积为
的面积为 C.
C. D.4
D.4
 ,则复数
,则复数 在复平面内对应的点位于( )
在复平面内对应的点位于( ) B.
B. C.
C. D.
D. .
. 是以1为首项的等比数列,若
是以1为首项的等比数列,若 ,则
,则 的值是 ( )
的值是 ( ) D.不确定
D.不确定  中,平面
中,平面 ⊥侧面
⊥侧面 .
. ;
; 与平面
与平面 ,二面角
,二面角 的大小为
的大小为  ,当
,当 时,求
时,求 的值.
的值.