Question

【题目】已知函数f（x）=ax2﹣x+2a﹣1（a＞0）．
（1）若f（x）在区间[1，2]为单调增函数，求a的取值范围；
（2）设函数f（x）在区间[1，2]上的最小值为g（a），求g（a）的表达式；
（3）设函数 ，若对任意x1 ， x2∈[1，2]，不等式f（x1）≥h（x2）恒成立，求实数a的取值范围．

Answer 1

【答案】
（1）解：∵函数f（x）=ax2﹣x+2a﹣1（a＞0）的图象是开口朝上，且以直线x= 为对称轴的抛物线，

若f（x）在区间[1，2]为单调增函数

则 ，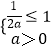

解得：

（2）解：①当0＜ ＜1，即a＞ 时，f（x）在区间[1，2]上为增函数，

此时g（a）=f（1）=3a﹣2

②当1≤ ≤2，即 时，f（x）在区间[1， ]是减函数，在区间[ ，2]上为增函数，

此时g（a）=f（ ）=

③当 ＞2，即0＜a＜ 时，f（x）在区间[1，2]上是减函数，

此时g（a）=f（2）=6a﹣3

综上所述：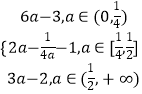

（3）解：对任意x1，x2∈[1，2]，不等式f（x1）≥h（x2）恒成立，

即f（x）min≥h（x）max，

由（2）知，f（x）min=g（a）

又因为函数 ，

所以函数h（x）在[1，2]上为单调减函数，所以 ，

①当 时，由g（a）≥h（x）max得： ，解得 ，（舍去）

②当 时，由g（a）≥h（x）max得： ，即8a2﹣2a﹣1≥0，

∴（4a+1）（2a﹣1）≥0，解得

所以

③当 时，由g（a）≥h（x）max得： ，解得 ，

所以a

综上所述：实数a的取值范围为

【解析】（1）若f（x）在区间[1，2]为单调增函数，则 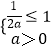，解得a的取值范围；（2）分类讨论给定区间与对称轴的关系，分析出各种情况下g（x）的表达式，综合讨论结果，可得答案；（3）不等式f（x1）≥h（x2）恒成立，即f（x）min≥h（x）max ， 分类讨论各种情况下实数a的取值，综合讨论结果，可得答案．