题目内容
(x+1)3+(x-2)8=a+a1(x-1)2+a2(x-1)2+…+a8(x-1)8,则a6= .
【答案】分析:[(x-1)+2]3展开式中不含(x-1)6项,[(x-1)-1]8中含(x-1)6项为T2+1=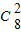 (x-1)6(-1)2,从而求出所求.
(x-1)6(-1)2,从而求出所求.
解答:解:(x+1)3+(x-2)8=[(x-1)+2]3+[(x-1)-1]8
[(x-1)+2]3展开式中不含(x-1)6项,[(x-1)-1]8中含(x-1)6项为T2+1=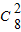 (x-1)6(-1)2
(x-1)6(-1)2
∴a6=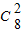 =28
=28
故答案为:28
点评:本题主要考查了二项式定理的应用,以及二项展开式的通项公式,求展开式中某项的系数,属于中档题.
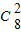 (x-1)6(-1)2,从而求出所求.
(x-1)6(-1)2,从而求出所求.解答:解:(x+1)3+(x-2)8=[(x-1)+2]3+[(x-1)-1]8
[(x-1)+2]3展开式中不含(x-1)6项,[(x-1)-1]8中含(x-1)6项为T2+1=
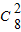 (x-1)6(-1)2
(x-1)6(-1)2∴a6=
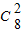 =28
=28故答案为:28
点评:本题主要考查了二项式定理的应用,以及二项展开式的通项公式,求展开式中某项的系数,属于中档题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 ;
; 的线性生成函数h(x),其中a>0,b>0.若h(x)≥b对a∈[1,2]恒成立,求实数b的取值范围.
的线性生成函数h(x),其中a>0,b>0.若h(x)≥b对a∈[1,2]恒成立,求实数b的取值范围. )=3f(
)=3f( )=3[1-|
)=3[1-| -2|]=1,f(54)=33f(
-2|]=1,f(54)=33f( )=27,请你根据以上信息,求出集合M={x|f(x)=f(99)}中最小的元素是 .
)=27,请你根据以上信息,求出集合M={x|f(x)=f(99)}中最小的元素是 .