题目内容
(本小题满分12分)
在平面 内,不等式
内,不等式 确定的平面区域为
确定的平面区域为 ,不等式组
,不等式组 确定的平面区域为
确定的平面区域为 .
.
(Ⅰ)定义横、纵坐标为整数的点为“整点”. 在区域 任取3个整点,求这些整点中恰有2个整点在区域
任取3个整点,求这些整点中恰有2个整点在区域 的概率;
的概率;
(Ⅱ)在区域 每次任取
每次任取 个点,连续取
个点,连续取 次,得到
次,得到 个点,记这
个点,记这 个点在区域
个点在区域 的个数为
的个数为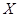 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
在平面
 内,不等式
内,不等式 确定的平面区域为
确定的平面区域为 ,不等式组
,不等式组 确定的平面区域为
确定的平面区域为 .
.(Ⅰ)定义横、纵坐标为整数的点为“整点”. 在区域
 任取3个整点,求这些整点中恰有2个整点在区域
任取3个整点,求这些整点中恰有2个整点在区域 的概率;
的概率;(Ⅱ)在区域
 每次任取
每次任取 个点,连续取
个点,连续取 次,得到
次,得到 个点,记这
个点,记这 个点在区域
个点在区域 的个数为
的个数为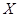 ,求
,求 的分布列和数学期望.
的分布列和数学期望.(Ⅰ) ;(Ⅱ)
;(Ⅱ)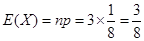 ).
).
 ;(Ⅱ)
;(Ⅱ)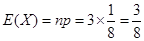 ).
).(1)画出平面区域 和平面区域
和平面区域 .可分别找到区域内的整点个数,由概率公式计算出恰有
.可分别找到区域内的整点个数,由概率公式计算出恰有
2个整点在区域 的概率;(2)本题属于几何概型,先求出平面区域
的概率;(2)本题属于几何概型,先求出平面区域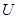 的面积和区域
的面积和区域 与区域
与区域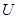 相交部
相交部
分的面积,由几何概型的概率公式得在区域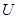 任取1个点,则该点在区域
任取1个点,则该点在区域 的概率的值,又随机变量
的概率的值,又随机变量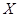 的可能取值为:
的可能取值为: .根据独立重复试验可分别求出对应的概率,列出分布列,根据期望公式计算出
.根据独立重复试验可分别求出对应的概率,列出分布列,根据期望公式计算出 的数学期望.
的数学期望.
(Ⅰ)依题可知平面区域 的整点为:
的整点为: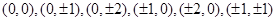 共有13个,上述整点在平面区域
共有13个,上述整点在平面区域 的为:
的为: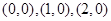 共有3个,
共有3个,
∴ . ……………………………………………………………(4分)
. ……………………………………………………………(4分)
(Ⅱ)依题可得,平面区域 的面积为
的面积为 ,
,
平面区域 与平面区域
与平面区域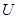 相交部分的面积为
相交部分的面积为 .
.
(设扇形区域中心角为 ,则
,则 得
得 ,也可用向量的夹角公式求
,也可用向量的夹角公式求 ).
).
在区域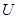 任取1个点,则该点在区域
任取1个点,则该点在区域 的概率为
的概率为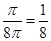 ,随机变量
,随机变量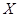 的可能取值为:
的可能取值为: .
.
 ,
,  ,
,
 ,
, 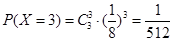 ,
,
∴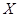 的分布列为
的分布列为
∴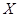 的数学期望:
的数学期望: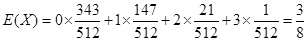 . ………………………(12分)
. ………………………(12分)
(或者: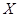 ~
~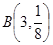 ,故
,故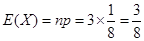 ).
).
 和平面区域
和平面区域 .可分别找到区域内的整点个数,由概率公式计算出恰有
.可分别找到区域内的整点个数,由概率公式计算出恰有2个整点在区域
 的概率;(2)本题属于几何概型,先求出平面区域
的概率;(2)本题属于几何概型,先求出平面区域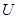 的面积和区域
的面积和区域 与区域
与区域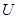 相交部
相交部分的面积,由几何概型的概率公式得在区域
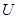 任取1个点,则该点在区域
任取1个点,则该点在区域 的概率的值,又随机变量
的概率的值,又随机变量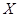 的可能取值为:
的可能取值为: .根据独立重复试验可分别求出对应的概率,列出分布列,根据期望公式计算出
.根据独立重复试验可分别求出对应的概率,列出分布列,根据期望公式计算出 的数学期望.
的数学期望.(Ⅰ)依题可知平面区域
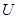 的整点为:
的整点为: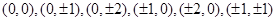 共有13个,上述整点在平面区域
共有13个,上述整点在平面区域 的为:
的为: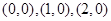 共有3个,
共有3个,∴
 . ……………………………………………………………(4分)
. ……………………………………………………………(4分)(Ⅱ)依题可得,平面区域
 的面积为
的面积为 ,
,平面区域
 与平面区域
与平面区域 相交部分的面积为
相交部分的面积为 .
.(设扇形区域中心角为
 ,则
,则 得
得 ,也可用向量的夹角公式求
,也可用向量的夹角公式求 ).
).在区域
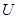 任取1个点,则该点在区域
任取1个点,则该点在区域 的概率为
的概率为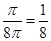 ,随机变量
,随机变量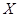 的可能取值为:
的可能取值为: .
. ,
,  ,
, ,
, 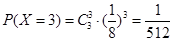 ,
,∴
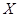 的分布列为
的分布列为  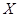 | 0 | 1 | 2 | 3 |
 | 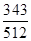 |  | 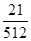 | 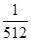 |
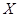 的数学期望:
的数学期望: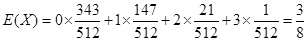 . ………………………(12分)
. ………………………(12分)(或者:
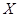 ~
~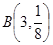 ,故
,故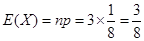 ).
).
练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
 的值.
的值.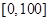 ,样本数据分组为
,样本数据分组为 ,
, ,
, ,
, ,
, .
. 的值;
的值; ,求
,求 ,求
,求 视觉
视觉 

 .
. ,求随机变量
,求随机变量 .
. ,其他三项挑战失败的概率分别为
,其他三项挑战失败的概率分别为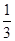 .
. ,规定使用“七局四胜制”,即先赢四局者胜.
,规定使用“七局四胜制”,即先赢四局者胜. ,Y为甲与乙命中10环次数的差的绝对值.
,Y为甲与乙命中10环次数的差的绝对值.  ,则
,则 ( )
( )


