题目内容
设曲线C：y=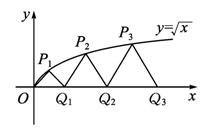
上的点Pn(n=1,2,3,…)与x轴上点构成正三角形OP1Q1，Q1P2Q2，Q2P3Q3，…，Qn-1PnQn,这些正三角形各边长依次设为a1,a2,a3,…an.
(1)求an的表达式；
(2)求证：a1+a2+a3+…+an=
.
解：（1）直线OP1方程为y=
x
解方程组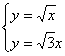 得P1（，
）∴ a1=2×
=
直线P2Q方程为y=
(x-
)
解方程组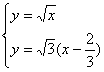
得P2（
，
）∴a2×
=
,a2=
猜想an=
用数学归纳法证明
①n=1时成立
②假设n=k(k≥2)时ak=
由a1+a2+…+ak=
·
=
直线Pk+1Qk方程为y=
［x-
］
解方程组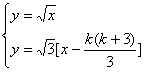
Pk+1(
,
(k+1))
∴ak+1·
=
(k+1),ak+1=
(k+1)
由①②知对n∈N+,an=
成立
（2）由a1+a2+…+an
=
+
+…+
=
(1+2+3+…+n)
=
·
=
练习册系列答案
阅读快车系列答案
相关题目
+
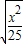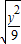=1上的点，F1（-4，0），F2（4，0），则|PF1|+|PF2|（ ）
+
=1上的点，F1（-4，0），F2（4，0），则|PF1|+|PF2|（ ）
+
=1上的点，F1（-4，0），F2（4，0），则|PF1|+|PF2|（ ）
+
=1上的点，F1（-4，0），F2（4，0），则|PF1|+|PF2|（ ）