题目内容
已知直线 过点
过点 ,当直线
,当直线 与圆
与圆 有两个交点时,其斜率k的取值范围是( )
有两个交点时,其斜率k的取值范围是( )
A . B.
B.  C.
C.
 D.
D.

【答案】
C
【解析】解:由已知中可得圆x2-2x+y2=0的圆心坐标为M(1,0),半径为1,
若直线l的斜率不存在,则直线l与圆相离,与题意不符;
故可设直线l的斜率为k,
则l:y=k(x+2)
代入圆x2-2x+y2=0的方程可得:
(k2+1)x2+(4k2-2)x+4k2=0…①
若直线l与圆有两个交点,则方程①有两个根
则△>0
解得 <k<
<k< .
.
选C

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 过点
过点 ,当直线
,当直线 有两个交点时,其斜率
有两个交点时,其斜率 的取值范围是
______________________.
的取值范围是
______________________. 过点
过点 ,当直线
,当直线 与圆
与圆 有两个交点时,其斜率
有两个交点时,其斜率 的取值范围是
的取值范围是 B.
B.  C.
C.
 D.
D.

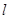 过点
过点 ,当直线
,当直线 有两个交点时,其斜率k的取值范围是
( )
有两个交点时,其斜率k的取值范围是
( ) B
B
 C
C  D
D 