题目内容

如图所示，已知椭圆C1和抛物线C2有公共焦点F(1，0)，C1的中心和C2的顶点都在坐标原点，过点M(4，0)的直线l与抛物线C2分别相交于A，B两点

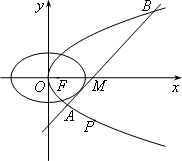
(1)写出抛物线C2的标准方程；

(2)若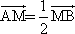，求直线l的方程；

(3)若坐标原点O关于直线l的对称点P在抛物线C2上，直线l与椭圆C1有公共点，求椭圆C1的长轴长的最小值．

答案：
解析：

　　(1)　　5分

　　(2)设

　　

　　　　

　　　　　10分

　　(3)设，坐标原点关于直线的对称点为，则

　　

　　设椭圆方程为

　　消元整理

　　　　　15分


练习册系列答案
相关题目
（文）如图所示：已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)，F1、F2为其左、右焦点，A为右顶点，过F1的直线l与椭圆相交于P、Q两点，且有
1
|PF1|
+
1
|QF|
=2．
（1）求椭圆长半轴长a的取值范围；
（2）若
AP
•
AQ
=a2且a∈(
4
3
，
9
5
)，求直线l的斜率的取值范围．
如图所示，已知椭圆C的离心率为
3
2
，A、B、F分别为椭圆的右顶点、上顶点、右焦点，且S△ABF=1-
3
2
．
（1）求椭圆C的方程；
（2）已知直线l：y=kx+m被圆O：x2+y2=4所截弦长为2
3
，若直线l与椭圆C交于M、N两点．求△OMN面积的最大值．
如图所示，已知椭圆C：x2+
y2
a2
=1（a＞1）的离心率为e，点F为其下焦点，点A为其上顶点，过F的直线l：y=mx-c（其中c=
a2-1
与椭圆C相交于P，Q两点，且满足
AP
•
AQ
=
a2(a+c)2-1
2-c2
．
（1）试用a表示m2；
（2）求e的最大值；
（3）若e∈（
1
3
，
1
2
），求m的取值范围．
如图所示，已知椭圆C：x2+
y2
a2
=1（a＞1）的离心率为e，点F为其下焦点，点A为其上顶点，过F的直线l：y=mx-c（其中c=
a2-1
与椭圆C相交于P，Q两点，且满足
AP
•
AQ
=
a2(a+c)2-1
2-c2
．
（1）试用a表示m2；
（2）求e的最大值；
（3）若e∈（
1
3
，
1
2
），求m的取值范围．
精英家教网
（文）如图所示：已知椭圆C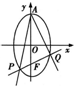：，F1、F2为其左、右焦点，A为右顶点，过F1的直线l与椭圆相交于P、Q两点，且有．
（1）求椭圆长半轴长a的取值范围；
（2）若，求直线l的斜率的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网