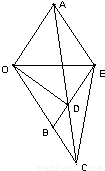
题目内容
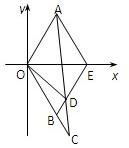 如图,△AOE和△BOE都是边长为1的等边三角形,延长OB到C使|BC|=t(t>0),连AC交BE于D点.
如图,△AOE和△BOE都是边长为1的等边三角形,延长OB到C使|BC|=t(t>0),连AC交BE于D点.(1)用t表示向量
| OC |
| OD |
(2)当
| OC |
| 3 |
| 2 |
| OB |
| OD |
| EC |
分析:(1)向量
可以直接由
来表示,求
,可以先求
转化为
,∵OA∥BE;
(2)求向量
和
的夹角的大小,只需求其数量积,坐标运算和公式形式运算,可以求出夹角.
| OC |
| OB |
| OD |
| AC |
| AD |
(2)求向量
| OD |
| EC |
解答: 解:(1)
解:(1)
=(
(t+1),-
(t+1)),
∵
=t
,
∴
=t
,
=
,又
=(
,
),
=
-
=(
t,-
(t+2));
∴
=(
,-
),
∴
=
+
=(
,-
).
(2)由已知t=
,∴
=(
,-
),
=(-
,-
)
∴
•
=-
+
=
又∵|
|=
,|
|=
=
∴cos<
,
>=
=
,
∴向量
与
的夹角为60°.
 解:(1)
解:(1)| OC |
| 1 |
| 2 |
| ||
| 2 |
∵
| BC |
| AE |
∴
| DC |
| AD |
| AD |
| 1 |
| 1+t |
| AC |
| OA |
| 1 |
| 2 |
| ||
| 2 |
| AC |
| OC |
| OA |
| 1 |
| 2 |
| ||
| 2 |
∴
| AD |
| t |
| 2(t+1) |
| ||
| 2(t+1) |
∴
| OD |
| OA |
| AD |
| 2t+1 |
| 2(t+1) |
| ||
| 2(t+1) |
(2)由已知t=
| 1 |
| 2 |
| OD |
| 2 |
| 3 |
| ||
| 3 |
| EC |
| 1 |
| 4 |
3
| ||
| 4 |
∴
| OD |
| EC |
| 1 |
| 6 |
| 3 |
| 4 |
| 7 |
| 12 |
又∵|
| OD |
| ||
| 3 |
| EC |
2
| ||
| 4 |
| ||
| 2 |
∴cos<
| OD |
| EC |
| ||
|
| 1 |
| 2 |
∴向量
| OD |
| EC |
点评:本题考查向量的数量积,坐标运算和向量数量积的两种计算,是中档题.

练习册系列答案
相关题目
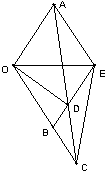 如图,△AOE和△BOE都是边长为1的等边三角形,延长OB到C使|BC|=t(t>0),连AC交BE于D点,则向量
如图,△AOE和△BOE都是边长为1的等边三角形,延长OB到C使|BC|=t(t>0),连AC交BE于D点,则向量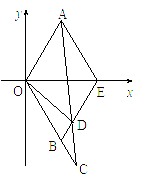
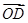 和
和 的夹角的大小为
.
的夹角的大小为
.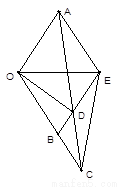
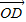 和
和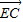 的夹角的大小为 .
的夹角的大小为 .