题目内容
已知函数 ,点
,点 、
、 在函数
在函数 的图象上,
的图象上,
点 在函数
在函数 的图象上,设
的图象上,设
 .
.
(1)求数列 的通项公式;
的通项公式;
(2)记 ,求数列
,求数列 的前
的前 项和为
项和为 ;
;
(3)已知 ,记数列
,记数列 的前
的前 项和为
项和为 ,数列
,数列 的前
的前 项和为
项和为 ,试比较
,试比较 与
与 的大小.
的大小.
 ,点
,点 、
、 在函数
在函数 的图象上,
的图象上,点
 在函数
在函数 的图象上,设
的图象上,设
 .
.(1)求数列
 的通项公式;
的通项公式;(2)记
 ,求数列
,求数列 的前
的前 项和为
项和为 ;
;(3)已知
 ,记数列
,记数列 的前
的前 项和为
项和为 ,数列
,数列 的前
的前 项和为
项和为 ,试比较
,试比较 与
与 的大小.
的大小.(1)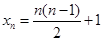 ;
;
(2)
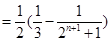 ;
;
(3)当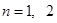 时,
时, ;
;
当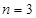 时,
时,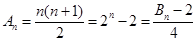 ;
;
当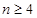 时,
时,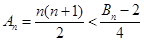 .
.
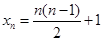 ;
;(2)

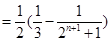 ;
;(3)当
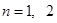 时,
时, ;
;当
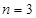 时,
时,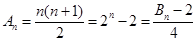 ;
;当
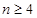 时,
时,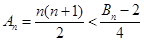 .
.试题分析:(1)把点点
 、
、 代入
代入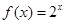 中,点
中,点 代入函数
代入函数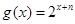 中,可得
中,可得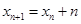 ,然后利用叠加的方法求的
,然后利用叠加的方法求的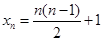 ;(2)由
;(2)由 和
和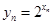 可得
可得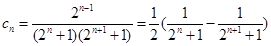 ,然后利用裂项法求数列
,然后利用裂项法求数列 的前
的前 项和
项和 即可;(3)由
即可;(3)由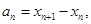 得
得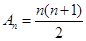 ,由
,由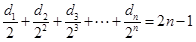 可得
可得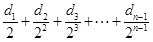
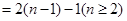
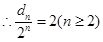 ,即
,即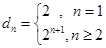 ,求出
,求出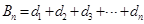
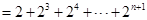
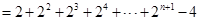 ,即
,即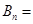
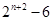 ,所以
,所以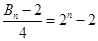 最后分类讨论比较
最后分类讨论比较 与
与 的大小即可.
的大小即可.试题解析:(1)由题有:
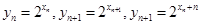
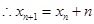
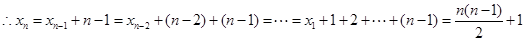 3分
3分(2)
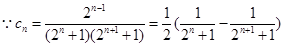 ,
,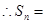
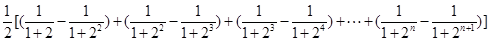
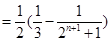 8分
8分(3)
 ,
,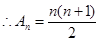 ,
,由
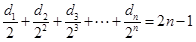 知
知
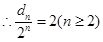 , 而
, 而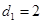 ,所以可得
,所以可得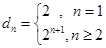 .
.于是
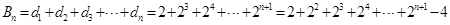
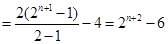 .
.
当
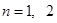 时
时  ;
;当
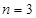 时,
时,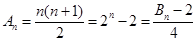
当
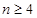 时,
时,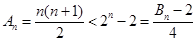
下面证明:当
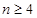 时,
时,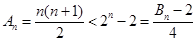
证法一:(利用组合恒等式放缩)
当
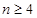 时,
时,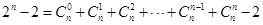
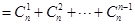
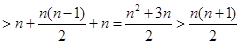
∴当
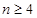 时,
时,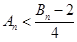 13分
13分 证法二:(数学归纳法)证明略
证法三:(函数法)∵
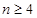 时,
时,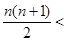
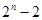
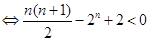
构造函数
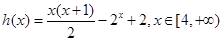 ,
,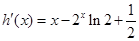
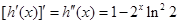 ∴当
∴当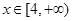 时,
时,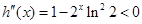
∴
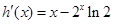 在区间
在区间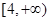 是减函数,
是减函数,∴当
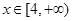 时,
时,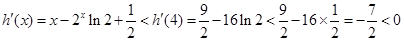
∴
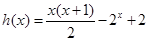 在区间
在区间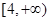 是减函数,
是减函数,∴当
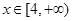 时,
时,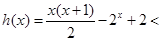
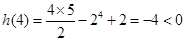
从而
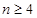 时,
时,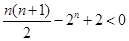 ,即
,即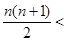
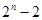 ∴当
∴当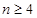 时,
时,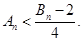

练习册系列答案
相关题目
 吨,此时所需生产费用为(
吨,此时所需生产费用为( )万元,当出售这种商品时,每吨价格为
)万元,当出售这种商品时,每吨价格为 万元,这里
万元,这里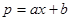 (
( 为常数,
为常数, )
)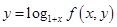 ,
, ,
, .
. 与
与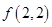 的大小;
的大小; ,证明:
,证明: ;
; 的图象为曲线
的图象为曲线 ,曲线
,曲线 处的切线斜率为
处的切线斜率为 ,若
,若 ,且存在实数
,且存在实数 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围. 从点
从点 出发,分别按逆时针方向沿周长均为
出发,分别按逆时针方向沿周长均为 的正三角形、正方形运动一周,
的正三角形、正方形运动一周, 两点连线的距离
两点连线的距离 与点
与点 走过的路程
走过的路程 的函数关系分别记为
的函数关系分别记为 ,定义函数
,定义函数 对于函数
对于函数 ,下列结论正确的个数是( )
,下列结论正确的个数是( )
 ;
; 的图像关于直线
的图像关于直线 对称;
对称; ;
; 上单调递增.
上单调递增. 满足
满足 ,则
,则 .
. (正常情况
(正常情况 ,且教职工平均月评价分数在50分左右,若有突出贡献可以高于100分)计算当月绩效工资
,且教职工平均月评价分数在50分左右,若有突出贡献可以高于100分)计算当月绩效工资 元.要求绩效工资不低于500元,不设上限且让大部分教职工绩效工资在600元左右,另外绩效工资越低、越高人数要越少.则下列函数最符合要求的是( )
元.要求绩效工资不低于500元,不设上限且让大部分教职工绩效工资在600元左右,另外绩效工资越低、越高人数要越少.则下列函数最符合要求的是( )



 的图象如图,则满足
的图象如图,则满足 的
的 的取值范 .
的取值范 .
 的定义域为
的定义域为 ,
, 且对于任意的
且对于任意的 都有
都有 ,若在区间
,若在区间 上函数
上函数 恰有四个不同零点,则实数
恰有四个不同零点,则实数 的取值范围为( )
的取值范围为( )



 ,则
,则 的值为 .
的值为 .