题目内容
已知向量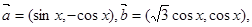 设函数
设函数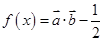 ;
;
(1)写出函数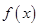 的单调递增区间;
的单调递增区间;
(2)若x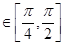 求函数
求函数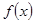 的最值及对应的x的值;
的最值及对应的x的值;
(3)若不等式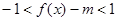 在x
在x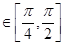 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
【答案】
解:(1)单调递增区间为 ;
;
(2)即 时,
时,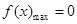 , 即
, 即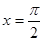 时,
时,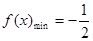 ;(3) (-1,
;(3) (-1,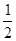 )
)
【解析】求三角函数的最值,周期,单调区间时需将三角函数的解析式化成正弦型的函数,然后在用整体法,令作用的角为一整体,如: 中令
中令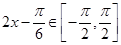 ,解得解集x;
,解得解集x;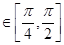
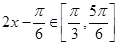 ,再数形结合,求得最值;若不等式
,再数形结合,求得最值;若不等式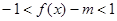 在x
在x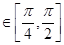 恒成立,一般在最值处成立即可,
恒成立,一般在最值处成立即可, 且
且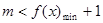 , 求出函数的最值带入。
, 求出函数的最值带入。
解:(1)由已知得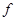 (x)=
(x)=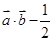 =
=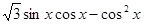 -
-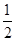
=

=
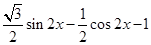 =
=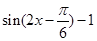 ……2分
……2分
由  得:
得: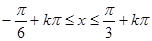
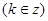
所以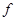 (x)=
(x)= 的单调递增区间为
的单调递增区间为
…… 4分
(2)由(1)知 ,
,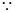 x
x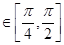 ,
,
所以 
故 当 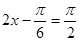 时,即
时,即 时,
时,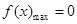
当 时,即
时,即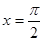 时,
时,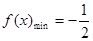 ……8分
……8分
(3)解法1
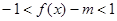
 (x
(x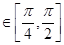 );
);
 且
且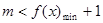 故m的范围为(-1,
故m的范围为(-1,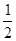 )
)
解法2: 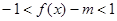
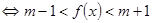

 且
且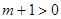 ;故m的范围为(-1,
;故m的范围为(-1,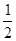 )
……12分
)
……12分

练习册系列答案
相关题目
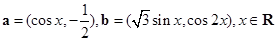 , 设函数
, 设函数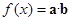 .
. 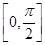 上的最大值和最小值.
上的最大值和最小值.  设函数
设函数
 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;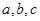 分别是角A、B、C的对边,若
分别是角A、B、C的对边,若 △ABC的面积为
△ABC的面积为 ,求
,求 的值.
的值.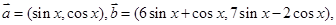
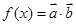
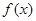 的最大值;
的最大值;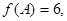 且
且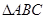 的面积为3,
的面积为3,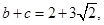 求a的值。
求a的值。 设函数
设函数 ;
;  的单调递增区间;
的单调递增区间;  求函数
求函数 的最值及对应的x的值;-
的最值及对应的x的值;- 在x
在x