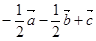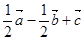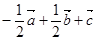题目内容
如图,四棱锥 的底面是正方形,
的底面是正方形,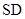 ⊥平面
⊥平面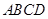 ,
,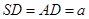 ,点E是SD上的点,且
,点E是SD上的点,且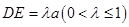 .
.
(1)求证:对任意的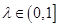 ,都有AC⊥BE;
,都有AC⊥BE;
(2)若二面角C-AE-D的大小为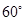 ,求
,求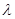 的值
的值
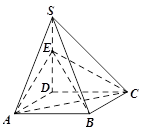
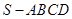 的底面是正方形,
的底面是正方形,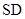 ⊥平面
⊥平面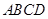 ,
,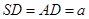 ,点E是SD上的点,且
,点E是SD上的点,且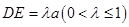 .
.(1)求证:对任意的
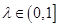 ,都有AC⊥BE;
,都有AC⊥BE;(2)若二面角C-AE-D的大小为
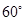 ,求
,求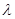 的值
的值
(1)如图建立空间直角坐标系 ,
,
则 ,
,
 ,
,
∴
 对任意
对任意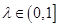 都成立,
都成立,
即AC⊥BE恒成立; ……………………6分
解:(2)显然 是平面
是平面 的一个法向量,
的一个法向量,
设平面 的一个法向量为
的一个法向量为 ,
,
∵ ,
,
∴ ,
,
取 ,则
,则 ,
, , ………………10分
, ………………10分
∵二面角C-AE-D的大小为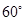 ,
,
∴ ,
,
∴ 为所求。
为所求。
 ,
,则
 ,
, ,
,∴

 对任意
对任意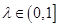 都成立,
都成立,即AC⊥BE恒成立; ……………………6分
解:(2)显然
 是平面
是平面 的一个法向量,
的一个法向量,设平面
 的一个法向量为
的一个法向量为 ,
,∵
 ,
,∴
 ,
,取
 ,则
,则 ,
, , ………………10分
, ………………10分∵二面角C-AE-D的大小为
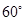 ,
,∴
 ,
,∴
 为所求。
为所求。略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,底面
,底面 中
中 ,棱
,棱 ,
, 分别为
分别为 的中点.
的中点.
 >的值;
>的值;
 ,且
,且 //(
//( ),则k=______.
),则k=______.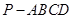 中,
中,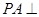 底面
底面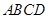 ,
,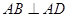 ,
,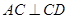 ,
,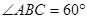
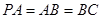 ,
, 是
是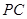 的中点.
的中点. ;
;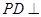 平面
平面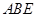 ;
;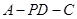 的正切值
的正切值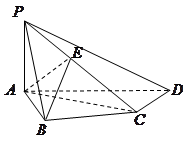
 图中未标出点G),求多面体P—AEFG的体积。
图中未标出点G),求多面体P—AEFG的体积。
 共线,则
共线,则 =
=  =
=  ,
, ,
, ,且
,且 ,则
,则 .
.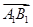 =
=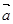 ,
, =
=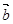 ,
,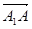 =
=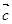 则下列向量中与
则下列向量中与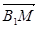 相等的向量是( )
相等的向量是( )