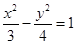题目内容
等轴双曲线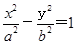 (a>0,b>0)的右焦点为F(c,0),方程
(a>0,b>0)的右焦点为F(c,0),方程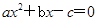 的实根分别为
的实根分别为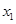 和
和 ,则三边长分别为|
,则三边长分别为|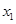 |,|
|,| |,2的三角形中,长度为2的边的对角是( )
|,2的三角形中,长度为2的边的对角是( )
| A.锐角 | B.直角 | C.钝角 | D.不能确定 |
C
解析试题分析:等轴双曲线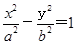 (
(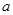 >0,b>0)的右焦点为F(c,0),可得
>0,b>0)的右焦点为F(c,0),可得 ,方程
,方程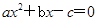 的实根分别为
的实根分别为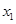 和
和 ,得
,得 ,长度为2的边的对角,由余弦定理可得
,长度为2的边的对角,由余弦定理可得
 ,故
,故 为钝角.
为钝角.
考点:本题等轴双曲线的定义及性质,根与系数关系,余弦定理,考查学生的基本运算能力以及转化与化归能力.

练习册系列答案
相关题目
过抛物线 的焦点且与直线
的焦点且与直线 平行的直线方程是( )
平行的直线方程是( )
A. | B. | C. | D. |
点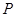 为双曲线
为双曲线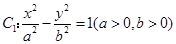 和圆
和圆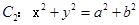 的一个交点,且
的一个交点,且 ,其中
,其中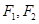 为双曲线
为双曲线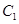 的两个焦点,则双曲线
的两个焦点,则双曲线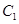 的离心率为( )
的离心率为( )
A.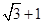 | B.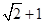 | C. | D.2 |
设双曲线 的两个焦点为
的两个焦点为 ,P是双曲线上的一点,且
,P是双曲线上的一点,且 ,则△PF1 F2的面积等于( )
,则△PF1 F2的面积等于( )
A.10 | B.8 | C.8 | D.16 |
已知双曲线 的离心率
的离心率 ,则它的渐近线方程为 ( )
,则它的渐近线方程为 ( )
A. | B. | C. | D. |
双曲线 的离心率为( )
的离心率为( )
A. | B. | C. | D. |
 的右焦点为
的右焦点为 ,过
,过 交双曲线的渐近线于
交双曲线的渐近线于 ,
, 两点,且与其中一条渐近线垂直,若
两点,且与其中一条渐近线垂直,若 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )


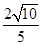
 的焦点为
的焦点为 ,已知点
,已知点 为抛物线上的两个动点,且满足
为抛物线上的两个动点,且满足 .过弦
.过弦 的中点
的中点 作抛物线准线的垂线
作抛物线准线的垂线 ,垂足为
,垂足为 ,则
,则 的最大值为( )
的最大值为( )




 的左、右焦点分别为
的左、右焦点分别为 ,以
,以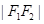 为直径的圆与双曲线渐近线的一个交点为
为直径的圆与双曲线渐近线的一个交点为 ,则此双曲线的方程为( )
,则此双曲线的方程为( )