题目内容
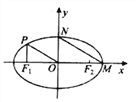
【题目】如图，椭圆
的左、右焦点为
，右顶点为
，上顶点为
，若
， 
与
轴垂直，且
.
（1）求椭圆方程；
（2）过点
且不垂直于坐标轴的直线与椭圆交于
两点，已知点
，当
时，求满足
的直线
的斜率
的取值范围.
【答案】(1) 
(2) 
【解析】试题分析：（1）由两条直线平行可得
，由点
在曲线上可得其纵坐标为
，由两者相等可得
，结合
，解出方程组即可；（2）设直线
的方程为： 
， 
， 
，与椭圆方程联立利用根与系数的关系得到
和
，线段
的垂直平分线方程为，求出与
轴的交，由交点横坐标列出不等式，解出即可得出结果.
试题解析：(1)设
，由
轴， 
知， 
，∴
，
又由
得
，∴
，∴
，
又
， 
，
∴
， 
，∴椭圆方程为
.
(2)设
， 
，直线
的方程为： 
，
联立
，得
， 
，
设线段
的垂直平分线方程为： 
.
令
，得
，
由题意知， 
为线段
的垂直平分线与
轴的交点，所以
，且
，所以
.
练习册系列答案
相关题目
