题目内容
判断函数f（x）=-x3+1在（-∞，+∞）上的单调性；
解：设x1，x2是R上任意两个值，且x1＜x2
则f（x1）-f（x2）=-x13+1-（-x23+1）=x23-x13
=（x2-x1）（x22+x1x2+x12）
=（x2-x1）[（x22+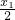
）2+
）]
∵x1，x2是R上任意两个值，且x1＜x2
∴（x2-x1）＞0，[（x22+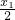）2+）]＞0
∴f（x1）＞f（x2）
∴y=f（x）是R上的减函数
分析：用定义法证明单调性，先设x1，x2是R上任意两个值，且x1＜x2，再对两个函数值作差，判断f（x1）-f（x2）的符号，做题时，对差进行合理的形式变换有利于函数值的符号的判断．
点评：本题考查字数的单调性的证明，本题用的定义法证明，作题时要注意做题步骤一取，二作差整理，三判号，四得出结论，本题为了判断符号的方便对差式进行变形的技巧很重要．
则f（x1）-f（x2）=-x13+1-（-x23+1）=x23-x13
=（x2-x1）（x22+x1x2+x12）
=（x2-x1）[（x2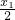2+
）2+）]∵x1，x2是R上任意两个值，且x1＜x2
∴（x2-x1）＞0，[（x22+
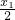）2+）]＞0∴f（x1）＞f（x2）
∴y=f（x）是R上的减函数
分析：用定义法证明单调性，先设x1，x2是R上任意两个值，且x1＜x2，再对两个函数值作差，判断f（x1）-f（x2）的符号，做题时，对差进行合理的形式变换有利于函数值的符号的判断．
点评：本题考查字数的单调性的证明，本题用的定义法证明，作题时要注意做题步骤一取，二作差整理，三判号，四得出结论，本题为了判断符号的方便对差式进行变形的技巧很重要．
练习册系列答案
相关题目