题目内容
有下列叙述①集合A=(m+2,2m﹣1)⊆B=(4,5),则m∈[2,3]②两向量平行,那么两向量的方向一定相同或者相反③若不等式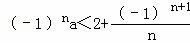 对任意正整数n恒成立,则实数a的取值范围是
对任意正整数n恒成立,则实数a的取值范围是
④对于任意两个正整数m,n,定义某种运算⊕如下:当m,n奇偶性相同时,m⊕n=m+n;当m,n奇偶性不同时,m⊕n=mn,在此定义下,集合M={(a,b)|a⊕b=12,a∈N+,b∈N+}中元素的个数是15个.上述说法正确的是 .
解:①∵集合A=(m+2,2m﹣1)⊆B=(4,5),∴ ,解得m∈[2,3];或m+2≥2m﹣1,解得m≤3,综上可知:m≤3,故不正确;②因为零向量与任何向量平行,故不正确;③当n为偶数时,原不等式可化为
,解得m∈[2,3];或m+2≥2m﹣1,解得m≤3,综上可知:m≤3,故不正确;②因为零向量与任何向量平行,故不正确;③当n为偶数时,原不等式可化为 ,∴a
,∴a ,即a<
,即a< ;当n为奇数时,原不等式可化为
;当n为奇数时,原不等式可化为 ,即
,即 ,∴a≥﹣2.综上可知:实数a的取值范围是
,∴a≥﹣2.综上可知:实数a的取值范围是 ,因此正确;④当a与b的奇偶性相同时,(a,b)可取(1,11),(2,10),(3,9),(4,8),(5,7),(6,6),(7,5),(8,4),(9,3),(10,2),(11,1)共11个;
,因此正确;④当a与b的奇偶性相同时,(a,b)可取(1,11),(2,10),(3,9),(4,8),(5,7),(6,6),(7,5),(8,4),(9,3),(10,2),(11,1)共11个;
.当a与b的奇偶性不相同时,(a,b)可取(1,12),(12,1),(3,4),(4,3).综上可知:集合M={(a,b)|a⊕b=12,a∈N+,b∈N+}中元素的个数是15个,因此正确.故正确的答案为③④.故答案为③④.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 时
时 恒成立,又
恒成立,又 的解集是 .
的解集是 . ,则集合A∩B= .
,则集合A∩B= .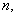 若
若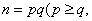 且
且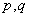 为整数),当
为整数),当 最小时,则称
最小时,则称 为
为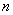 的“最佳分解”,并规定
的“最佳分解”,并规定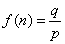 (如12的分解有
(如12的分解有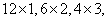 其中,
其中,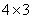 为12的最佳分解,则
为12的最佳分解,则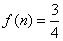 )。关于
)。关于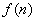 有下列判断:①
有下列判断:①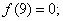 ②
②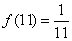 ;③
;③ ④
④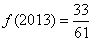 。其中,正确判断的序号是 .
。其中,正确判断的序号是 .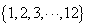 ,此集合的符合如下条件的子集的数目为
,此集合的符合如下条件的子集的数目为 :子集均含有4个元素,且这4个元素至少有两个是连续的.则
:子集均含有4个元素,且这4个元素至少有两个是连续的.则 在区间
在区间 内单调递增,则a的取值范围是( )
内单调递增,则a的取值范围是( ) B.
B. C.
C. D.
D.
 的最小值为
的最小值为  的最大值为
的最大值为 ,最小值为
,最小值为 ,最小正周期为
,最小正周期为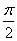 ,直线
,直线 是其图像的一条对称轴,则符合条件的解析式为A .
是其图像的一条对称轴,则符合条件的解析式为A .  B.
B. 
 D.
D. 