题目内容
8.设两个非零向量$\overrightarrow{{e}_{1}}$与$\overrightarrow{{e}_{2}}$不共线,且$\overrightarrow{AB}$=2$\overrightarrow{{e}_{1}}$+k$\overrightarrow{{e}_{2}}$,$\overrightarrow{CB}$=$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$,$\overrightarrow{CD}$=2$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$,若A,B,D三点共线,则k的值为0.分析 由向量$\overrightarrow{CB}$、$\overrightarrow{CD}$表示出$\overrightarrow{BD}$,再由A,B,D三点共线得出$\overrightarrow{AB}$=λ$\overrightarrow{BD}$,从而求出k的值.
解答 解:两个非零向量$\overrightarrow{{e}_{1}}$与$\overrightarrow{{e}_{2}}$不共线,$\overrightarrow{AB}$=2$\overrightarrow{{e}_{1}}$+k$\overrightarrow{{e}_{2}}$,
$\overrightarrow{CB}$=$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$,$\overrightarrow{CD}$=2$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$,
∴$\overrightarrow{BD}$=$\overrightarrow{CD}$-$\overrightarrow{CB}$=$\overrightarrow{{e}_{1}}$;
又A,B,D三点共线,
∴$\overrightarrow{AB}$=λ$\overrightarrow{BD}$,
即2$\overrightarrow{{e}_{1}}$+k$\overrightarrow{{e}_{2}}$=λ$\overrightarrow{{e}_{1}}$,
解得k=0.
点评 本题考查了应用平面向量的共线定理解决三点共线的问题,是基础题目.

练习册系列答案
相关题目
1.下列函数在区间(0,+∞)上是减函数的是( )
| A. | f(x)=3x-2 | B. | f(x)=9-x2 | C. | $f(x)=\frac{1}{x-1}$ | D. | f(x)=log2x |
2.下列各式的大小关系正确的是( )
| A. | sin11°>sin168° | B. | sin194°<cos160° | ||
| C. | cos(-$\frac{15π}{8}$)>cos$\frac{14π}{9}$ | D. | tan(-$\frac{π}{5}$)<tan(-$\frac{3π}{7}$) |
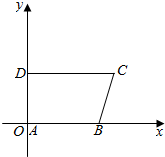 设直角梯形ABCD,DA⊥AB,在两平行边AB、DC上有两个动点P、Q,直线PQ平分梯形的面积,求证:PQ必过一个定点.
设直角梯形ABCD,DA⊥AB,在两平行边AB、DC上有两个动点P、Q,直线PQ平分梯形的面积,求证:PQ必过一个定点.