题目内容
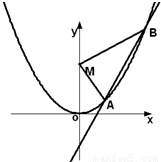
 如图,已知直线l:y=kx-2与抛物线C:x2=-2py(p>0)交于A,B两点,O为坐标原点,
如图,已知直线l:y=kx-2与抛物线C:x2=-2py(p>0)交于A,B两点,O为坐标原点,| OA |
| OB |
(Ⅰ)求直线l和抛物线C的方程;
(Ⅱ)抛物线上一动点P从A到B运动时,求△ABP面积最大值.
分析:(Ⅰ)把直线与抛物线方程联立,设出A,B的坐标,利用韦达定理表示出x1+x2,进而根据直线方程求得y1+y2的表达式,然后利用
+
=(-4,-12)求得p和k,则直线l和抛物线C的方程可得.
(Ⅱ)设P(x0,y0),依题意,抛物线过P的切线与l平行时,△APB面积最大;对抛物线方程求导,求得x0,代入抛物线方程求得y0,点P的坐标可得,进而利用点到直线的距离求得P到直线l的距离把直线方程与抛物线方程联立,利用弦长公式求得|AB|,最后求得∴△ABP的面积最大值.
| OA |
| OB |
(Ⅱ)设P(x0,y0),依题意,抛物线过P的切线与l平行时,△APB面积最大;对抛物线方程求导,求得x0,代入抛物线方程求得y0,点P的坐标可得,进而利用点到直线的距离求得P到直线l的距离把直线方程与抛物线方程联立,利用弦长公式求得|AB|,最后求得∴△ABP的面积最大值.
解答:解:(Ⅰ)由
得,x2+2pkx-4p=0,
设A(x1,y1),B(x2,y2),则x1+x2=-2pk,y1+y2=k(x1+x2)-4=-2pk2-4,
因为
+
=(x1+x2,y1+y2)=(-2pk,-2pk2-4)=(-4,-12),
所以
解得
所以直线l的方程为y=2x-2,抛物线C的方程为x2=-2y
(Ⅱ)设P(x0,y0),依题意,抛物线过P的切线与l平行时,△APB面积最大,y′=-x,所以-x0=2?x0=-2,y0=-
x02=-2,所以P(-2,-2).
此时P到直线l的距离d=
=
=
,
由
得,x2+4x-4=0,
|AB|=
=
=4
∴△ABP的面积最大值为
=8
.
|
设A(x1,y1),B(x2,y2),则x1+x2=-2pk,y1+y2=k(x1+x2)-4=-2pk2-4,
因为
| OA |
| OB |
所以
|
|
所以直线l的方程为y=2x-2,抛物线C的方程为x2=-2y
(Ⅱ)设P(x0,y0),依题意,抛物线过P的切线与l平行时,△APB面积最大,y′=-x,所以-x0=2?x0=-2,y0=-
| 1 |
| 2 |
此时P到直线l的距离d=
| |2•(-2)-(-2)-2| | ||
|
| 4 | ||
|
4
| ||
| 5 |
由
|
|AB|=
| 1+k2 |
| (x1+x2)2-4x1•x2 |
| 1+22 |
| (-4)2-4(-4) |
| 10 |
∴△ABP的面积最大值为
4
| ||||||
| 2 |
| 2 |
点评:本题主要考查了直线与圆锥曲线的综合问题.解题时充分挖掘题目的隐含条件,寻找量与量间的关系灵活转化,解决问题.

练习册系列答案
相关题目
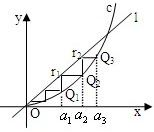 设a>0,如图,已知直线l:y=ax及曲线C:y=x2,C上的点Q1的横坐标为a1(0<a1<a).从C上的点Qn(n≥1)作直线平行于x轴,交直线l于点Pn+1,再从点Pn+1作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列{an}.
设a>0,如图,已知直线l:y=ax及曲线C:y=x2,C上的点Q1的横坐标为a1(0<a1<a).从C上的点Qn(n≥1)作直线平行于x轴,交直线l于点Pn+1,再从点Pn+1作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列{an}.
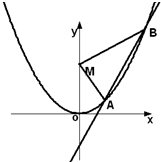 如图,已知直线L:y=kx-1与抛物线C:y=x2,相交于两点A、B,设点M(0,2),△MAB的面积为S.
如图,已知直线L:y=kx-1与抛物线C:y=x2,相交于两点A、B,设点M(0,2),△MAB的面积为S.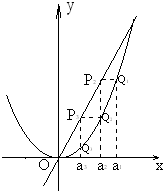 (2013•广州三模)如图,已知直线l:y=4x及曲线C:y=x2,C上的点Q1的横坐标为a1(0<a1<4).从曲线C上的点Qn(n≥1)作直线平行于x轴,交直线l于点Pn+1,再从点Pn+1作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列{an}.
(2013•广州三模)如图,已知直线l:y=4x及曲线C:y=x2,C上的点Q1的横坐标为a1(0<a1<4).从曲线C上的点Qn(n≥1)作直线平行于x轴,交直线l于点Pn+1,再从点Pn+1作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列{an}.