题目内容

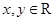(本题满分14分) 已知函数是定义域上的奇函数,且;函数是上的增函数，且对任意，总有

(Ⅰ)函数的解析式;

(Ⅱ)判断函数在上的单调性,并加以证明;

(Ⅲ)若,求实数的取值范围.

 

【答案】

 

(1)

(2)略

(3)

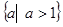
【解析】

解（Ⅰ)∵是奇函数,

∴对定义域内的任意的,都有,

即

整理得：  

 ∴   

又∵

∴,解得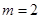                   

∴所求解析式为…………………………………4分

（Ⅱ)由Ⅰ)可得

  任取,

则由于

∴

令得 

∴

 又函数的定义域为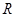

∴为奇函数

∵又

∴

∴即为

∴又函数是上的增函数

∴得 

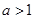
∴的取值范围是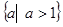……………………………………14分

 

 

练习册系列答案
相关题目
（本题满分14分
A．选修4-4：极坐标与参数方程在极坐标系中，直线l 的极坐标方程为θ=
π
3
 （ρ∈R ），以极点为坐标原点，极轴为x轴的正半轴建立平面直角坐标系，曲线C的参数方程为
x=2cosα
y=1+cos2α
 （α 参数）．求直线l 和曲线C的交点P的直角坐标．
B．选修4-5：不等式选讲
设实数x，y，z 满足x+y+2z=6，求x2+y2+z2 的最小值，并求此时x，y，z 的值．

（本题满分14分）如图，四边形ABCD为矩形，AD⊥平面ABE，AE＝EB＝BC＝2，为上的点，且BF⊥平面ACE．

（1）求证：AE⊥BE；（2）求三棱锥D－AEC的体积；（3）设M在线段AB上，且满足AM＝2MB，试在线段CE上确定一点N，使得MN∥平面DAE.

(本题满分14分)已知集合A={x|x2-2x-3≤0，x∈R}，B={x|x2-2mx+m2-4≤0，x∈R，m∈R}

(Ⅰ)若AB=[0,3]，求实数m的值

(Ⅱ)若ACRB，求实数m的取值范围

 

(本题满分14分)

已知点是⊙：上的任意一点，过作垂直轴于,动点满足。

（1）求动点的轨迹方程； 

（2）已知点，在动点的轨迹上是否存在两个不重合的两点、，使 (O是坐标原点)，若存在，求出直线的方程，若不存在，请说明理由。

 

(本题满分14分)已知函数.

(1)求函数的定义域；

(2)判断的奇偶性；

(3)方程是否有根?如果有根，请求出一个长度为的区间，使

；如果没有，请说明理由?(注：区间的长度为).

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网