题目内容
对于曲线y=f(x),若存在直线l使得曲线y=f(x)位于直线l的同一侧,则称曲线y=f(x)为半面曲线,下列曲线中是半面曲线的序号为 .(填上所有正确的序号)
①y=
②y=x3 ③y=x4+x3 ④y=x+
⑤y=1-x2+xsinx.
①y=
| 1 |
| x |
| 1 |
| x |
考点:函数的图象
专题:函数的性质及应用
分析:根据新定义,关键是判断每个函数是否有最值,通过最值即可判断是否存在直线I使得曲线 y=f(x)位于直线l的同一侧,则称曲线y=f(x)为半面曲线
解答:
解:①y=
的定义域为和值域均为(-∞,0)∪(0,+∞)无最大值或最小值,故不存在
②y=x3的定义域为和值域均为R,无最大值或最小值,故不存在
③∵y=x4+x3,y′=4x3+3x2=x2(4x+3),
令y′=0,解得x=0,或x=-
,
当y′>0,即x>-,函数单调递增,
当y′<0,即x>-
,函数单调递减,
故当x=-
,函数有最小值,
故存在直线I使得曲线 y=f(x)位于直线l的同一侧
④y=x+
无最大值或最小值,故不存在
⑤y=1-x2+xsinx,
当x趋向于无穷时,y的值趋向于负无穷,
当x趋向于0时,y=1,
故函数y=1-x2+xsinx,有最大值,
故存在直线I使得曲线 y=f(x)位于直线l的同一侧
函数的图象如图所示
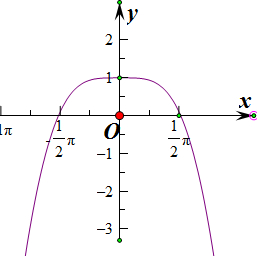
故答案为:③⑤
| 1 |
| x |
②y=x3的定义域为和值域均为R,无最大值或最小值,故不存在
③∵y=x4+x3,y′=4x3+3x2=x2(4x+3),
令y′=0,解得x=0,或x=-
| 3 |
| 4 |
当y′>0,即x>-,函数单调递增,
当y′<0,即x>-
| 3 |
| 4 |
故当x=-
| 3 |
| 4 |
故存在直线I使得曲线 y=f(x)位于直线l的同一侧
④y=x+
| 1 |
| x |
⑤y=1-x2+xsinx,
当x趋向于无穷时,y的值趋向于负无穷,
当x趋向于0时,y=1,
故函数y=1-x2+xsinx,有最大值,
故存在直线I使得曲线 y=f(x)位于直线l的同一侧
函数的图象如图所示

故答案为:③⑤
点评:本题考查了新定义,主要是求出函数的最值,属于中档题

练习册系列答案
相关题目
过点A(4,1)的圆C与直线x-y-1=0相切于点B(2,1),则圆C的方程是( )
| A、(x-5)2+y2=2 |
| B、(x-3)2+y2=4 |
| C、(x-5)2+y2=4 |
| D、(x-3)2+y2=2 |
函数y=log3(x-1)+
的定义域为( )
| 2-x |
| A、(1,2] |
| B、(1,+∞) |
| C、(2,+∞) |
| D、(-∞,0) |
