题目内容
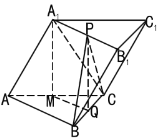
【题目】已知斜三棱柱![]() 的侧面
的侧面![]() 与底面
与底面![]() 垂直,
垂直,![]() ,
,![]() ,且
,且![]() ,
,![]() ,求:
,求:
(1)侧棱![]() 与底面
与底面![]() 所成角的大小;
所成角的大小;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.

【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由已知得直线![]() 在底面
在底面![]() 内的射影为直线
内的射影为直线![]() ,得
,得![]() 为侧棱
为侧棱![]() 与底面
与底面![]() 所成的角,由此能求出侧棱
所成的角,由此能求出侧棱![]() 与底面
与底面![]() 所成角的大小.
所成角的大小.
(2)求点![]() 到平面
到平面![]() 的距离也是求点
的距离也是求点![]() 到平面
到平面![]() 的距离,再用等体积法
的距离,再用等体积法![]() ,求出三棱锥
,求出三棱锥![]() 的高就是求出点
的高就是求出点![]() 到平面
到平面![]() 的距离.
的距离.
解:(1)取![]() 中点
中点![]() ,连接
,连接![]()
∵平面![]()
![]() 平面
平面![]() 平面
平面![]() 平面
平面![]() ,
,
又因为![]() ,所以
,所以![]() 又
又![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() 为
为![]() 在平面
在平面![]() 上的射影,所以
上的射影,所以![]() 为
为![]() 与平面
与平面![]() 所成的角
所成的角
∵![]() 且
且![]() ,∴
,∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]()
所以![]() 与平面
与平面![]() 所成的角为
所成的角为![]() 。
。
(2)取![]() 中点
中点![]() ,
,![]() 中点
中点![]() ,连接
,连接![]()
∵![]() ∴
∴![]() 平面
平面![]() ∴
∴![]() 且
且![]()
∴![]() 平面
平面![]() ∴
∴![]() ∴
∴![]()
在直角三角形![]() 中,由
中,由![]() ,得
,得![]()
∴![]() ∴
∴![]()
设点![]() 到平面
到平面![]() 得距离为
得距离为![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() 到平面
到平面![]() 得距离与
得距离与![]() 到平面
到平面![]() 的距离相等,
的距离相等,
∵![]() 平面
平面![]() ∴
∴![]() 平面
平面![]() ∴
∴![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
由![]() ,得
,得![]() ……①
……①
而![]() ,
,![]() ,
,![]()
将数据代入①式得![]() ,
,![]() ,
,
即![]() 到平面
到平面![]() 的距离为
的距离为![]() 。
。
故得解.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据
(吨)标准煤的几组对照数据
|
|
|
|
|
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式: