题目内容
设函数f(x)＝ex＋x－2，g(x)＝ln x＋x2－3.若实数a，b满足f(a)＝0，g(b)＝0，则 ( )．
| A．g(a)<0<f(b) | B．f(b)<0<g(a) |
| C．0<g(a)<f(b) | D．f(b)<g(a)<0 |
A
解析
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
曲线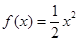
在点
处的切线方程为（ ）
A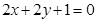． | B． |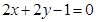
C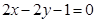． | D． |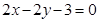
定义在R上的函数
满足
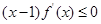，且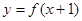
为偶函数，当
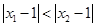时，有（ ）
A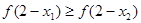． | B． |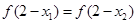
C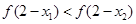． | D． |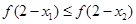
由曲线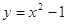
，直线
，
和
轴围成的封闭图形的面积（如图）可表示为（ ）
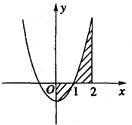
A． | B． |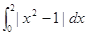
C． | D． |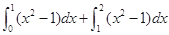
已知函数
的图象在
处的切线斜率为
（
），且当
时，其图象经过
，则
（ ）
A． | B． | C． | D． |
已知函数
是R上的可导函数，当
时，有
,则函数
的零点个数是( )
| A．0 | B．1 | C．2 | D．3 |
函数y=xlnx在区间(0,1)上是( )
| A．单调增函数 |
B．在(0, )上是减函数,在(,1)上是增函数 |
| C．单调减函数 |
| D．在(0,)上是增函数,在(,1)上是减函数 |
已知函数f(x)＝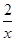
＋xln x，则曲线y＝f(x)在x＝1处的切线方程为( )
| A．x－y－3＝0 | B．x－y＋3＝0 | C．x＋y－3＝0 | D．x＋y＋3＝0 |
设函数f(x)满足x2f′(x)＋2xf(x)＝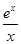
，f(2)＝
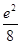，则x＞0时，f(x)( )．
| A．有极大值，无极小值 |
| B．有极小值，无极大值 |
| C．既有极大值又有极小值 |
| D．既无极大值也无极小值 |