题目内容
已知函数f(x)=x3-3x。
(Ⅰ)若曲线y=f(x)与直线y=m有且只有一个公共点,求m的取值范围;
(Ⅱ)过点P(2,-6)作曲线y=f(x)的切线,求此切线的方程。
(Ⅰ)若曲线y=f(x)与直线y=m有且只有一个公共点,求m的取值范围;
(Ⅱ)过点P(2,-6)作曲线y=f(x)的切线,求此切线的方程。
解:(Ⅰ)∵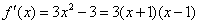 ,
,
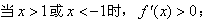

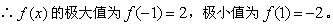
∵曲线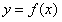 与直线y=m只有一个公共点,
与直线y=m只有一个公共点,
根据图象知,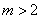 或
或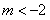 。
。
(Ⅱ)设切点坐标为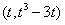 ,
,
则切线方程为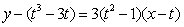 ,
,
∵切线过点P(2,-6),
∴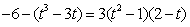 ,
,
化简,得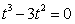 ,
,
∴t=0或t=3,
∴所求的切线方程为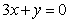 或
或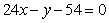 。
。
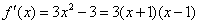 ,
,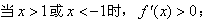

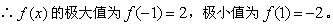
∵曲线
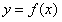 与直线y=m只有一个公共点,
与直线y=m只有一个公共点,根据图象知,
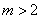 或
或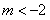 。
。 (Ⅱ)设切点坐标为
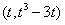 ,
,则切线方程为
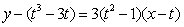 ,
,∵切线过点P(2,-6),
∴
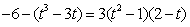 ,
,化简,得
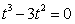 ,
,∴t=0或t=3,
∴所求的切线方程为
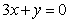 或
或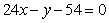 。
。
练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|