题目内容
已知函数f(n)= 且an=f(n)+f(n+1),则a1+a2+a3+…+a100等于( )
且an=f(n)+f(n+1),则a1+a2+a3+…+a100等于( )
(A)-100 (B)100 (C)-1020 (D)1020
B解析:当n为奇数时,an=n2-(n+1)2=-(2n+1).
当n为偶数时,an=-n2+(n+1)2=2n+1.
∴a1+a2+a3+…+a100=-3+5-7+9-…-199+201
=(-3+5)+(-7+9)+…+(-199+201)
=2×50=100.

练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,则
,则 ( )
( ) ,若数列{f(n)}(n∈N*)的前n项和等于
,若数列{f(n)}(n∈N*)的前n项和等于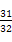 ,则n等于( )
,则n等于( ) ,
, ,
, ,
, ,…,
,…, 的前n项和为 .
的前n项和为 . 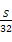 (B)
(B)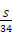 (C)
(C)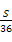 (D)
(D)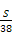
 .
. ,
, 为何值时,
为何值时, 有最小值?并求出最小值.
有最小值?并求出最小值.  且对于
且对于 ,都有
,都有 成立.求实数
成立.求实数 的取值范围.
的取值范围.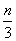 ,n∈N*.
,n∈N*.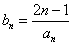 ,求数列{bn}的前n项和Sn
,求数列{bn}的前n项和Sn