题目内容
某市地铁全线共有四个车站,甲、乙两人同时在地铁第1号车站(首发站)乘车,假设每人自第2号站开始,在每个车站下车是等可能的,约定用有序实数对 表示“甲在
表示“甲在 号车站下车,乙在
号车站下车,乙在 号车站下车”
号车站下车”
(Ⅰ)用有序实数对把甲、乙两人下车的所有可能的结果列举出来;
(Ⅱ)求甲、乙两人同在第3号车站下车的概率;
(Ⅲ)求甲、乙两人在不同的车站下车的概率.
【答案】
(Ⅰ)(2,2)、(2,3)、(2,4)、(3,2)、
(3,3)、(3,4)、(4,2)、(4,3)、(4,4)(Ⅱ) (Ⅲ)
(Ⅲ)
【解析】
试题分析:(Ⅰ)甲、乙两人下车的所有可能的结果有:(2,2)、(2,3)、(2,4)、(3,2)、
(3,3)、(3,4)、(4,2)、(4,3)、(4,4)共9种 4分
(Ⅱ)设甲、乙两人同时在第3节车站下车为事件A,则 8分
8分
(Ⅲ)甲、乙两人在同一地铁站下车的基本事件有
(2,2)、(3,3)、(4,4)共3种,所求概率为 12分
12分
考点:概率
点评:第二问的概率可以借助于第一问的基本事件求古典概型概率或看做两个相互独立事件同时发生的概率,第三问直接考虑情况较多因此可先求其对立事件概率

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 表示“甲在
表示“甲在 号车站下车,乙在
号车站下车,乙在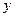 号车站下车”。
号车站下车”。 表示“甲在
表示“甲在 号车站下车,乙在
号车站下车,乙在 号车站下车”
号车站下车”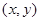 表示“甲在
表示“甲在 号车站下车,乙在
号车站下车,乙在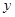 号车站下车”.
号车站下车”.