题目内容
设x,y满足约束条件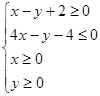 ,若目标函数
,若目标函数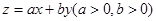 的最大值为6,则
的最大值为6,则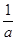 +
+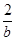 的最小值为
的最小值为
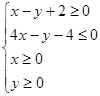 ,若目标函数
,若目标函数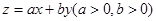 的最大值为6,则
的最大值为6,则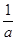 +
+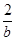 的最小值为
的最小值为| A.1 | B.3 | C.2 | D.4 |
B
试题分析:画出可行域,因为
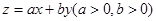 ,所以其经过点A(2,4)时,目标函数取到最大值6,即2a+4b=6,所以
,所以其经过点A(2,4)时,目标函数取到最大值6,即2a+4b=6,所以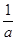 +
+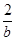 =
=
 ,故选B。
,故选B。
点评:小综合题,像
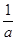 +
+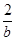 这类式子求最值问题,一般要探寻a,b的相关和式为定值,利用均值定理求解。利用均值定理要注意“一正、二定、三相等”。
这类式子求最值问题,一般要探寻a,b的相关和式为定值,利用均值定理求解。利用均值定理要注意“一正、二定、三相等”。
练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
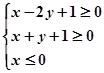 ,则x+2y的最大值是( )
,则x+2y的最大值是( )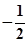
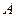 、
、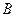 、
、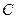 三种规格的成品.每
三种规格的成品.每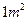 ,第二张为
,第二张为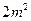 .今需要
.今需要 ,
, ,求
,求 的范围.
的范围. ,则t=x-y的取值范围是
,则t=x-y的取值范围是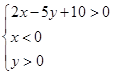 表示的平面区域内的整点坐标是 .
表示的平面区域内的整点坐标是 .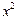 +
+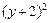 =1上,点M(x,y)在平面区域
=1上,点M(x,y)在平面区域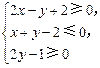 上,则AM的最小值是 .
上,则AM的最小值是 . 的取值范围是 .
的取值范围是 .