题目内容
某蔬菜基地种植甲、乙两种无公害蔬菜,生产一吨甲种蔬菜需用电力9千瓦时,耗肥4吨;生产一吨乙种蔬菜需用电力5千瓦时,耗肥5吨。现该基地仅有电力390千瓦时,肥240吨。已知生产一吨甲种蔬菜获利700元,生产一吨乙种蔬菜获利500元,在上述电力、肥的限制下,问如何安排甲、乙两种蔬菜种植,才能使利润最大?最大利润是多少?
解:设种植甲种蔬菜 吨,乙种蔬菜
吨,乙种蔬菜 吨,
吨,
利润为 元,根据题意可的得
元,根据题意可的得

 ……………………………(3分)目标函数为:
……………………………(3分)目标函数为: ………………(4分)
………………(4分)
作出二元一次不等式表示的平面区域,即可行域: ………………………(7分)
作直线: 即
即 平移直线,当直线过P点时目标函数取最大值
平移直线,当直线过P点时目标函数取最大值
解方程组 得
得
∴点A的坐标为
 …………………………………(10分)
…………………………………(10分)
∴ …………………………………………………(11分)
…………………………………………………(11分)
答:种植甲种蔬菜30吨,乙种蔬菜24吨,才能使利润最大,最大利润为33000元.(12分)
 吨,乙种蔬菜
吨,乙种蔬菜 吨,
吨,利润为
 元,根据题意可的得
元,根据题意可的得
|
 ……………………………(3分)目标函数为:
……………………………(3分)目标函数为: ………………(4分)
………………(4分)作出二元一次不等式表示的平面区域,即可行域: ………………………(7分)
作直线:
 即
即 平移直线,当直线过P点时目标函数取最大值
平移直线,当直线过P点时目标函数取最大值解方程组
 得
得
∴点A的坐标为

 …………………………………(10分)
…………………………………(10分)∴
 …………………………………………………(11分)
…………………………………………………(11分)答:种植甲种蔬菜30吨,乙种蔬菜24吨,才能使利润最大,最大利润为33000元.(12分)
略

练习册系列答案
相关题目
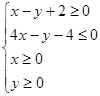 ,若目标函数
,若目标函数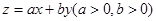 的最大值为6,则
的最大值为6,则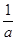 +
+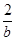 的最小值为
的最小值为 、
、 满足约束条件
满足约束条件 ,则
,则 的最大值是
的最大值是 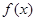 的定义域为
的定义域为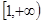 ,且
,且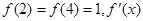 为
为 的图象如图所示.则不等式组
的图象如图所示.则不等式组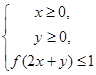 所表示的平面区域的面积是
所表示的平面区域的面积是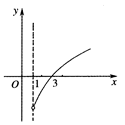

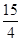
 满足
满足 ,则
,则 的最小值为 。
的最小值为 。 ,则
,则 的最大值为 。
的最大值为 。 满足约束条件
满足约束条件 ,则
,则 的最小值是 .
的最小值是 .
 是一个梯形,则实数
是一个梯形,则实数 的取值范围是[ ▲ .
的取值范围是[ ▲ .