Question

抛物线y=x²-4x+3及其在点A（1，0）和B（3，0）处的两条切线所围成图形的面积为（　　）

• A．

  2

  3

• B．

  4

  3

• C．2
• D．

  8

  3

Answer 1

分析：欲求切线的方程，只须求出其斜率的值即可，故先利用导数求出在切点处的导函数值，再结合A（1，0），B（3，0）都在抛物线上，即可求出切线的方程，然后可得直线与抛物线的交点的坐标和两切线与x轴交点的坐标，最后根据定积分在求面积中的应用公式即可求得所围成的面积S即可．

解答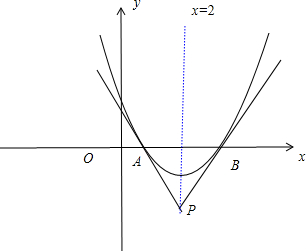：解：对y=x²-4x+3求导可得，y′=2x-4
∴抛物线y=x²-4x+3及其在点A（1，0）和B（3，0）处的两条切线的斜率分别为-2，2
从而可得抛物线y=x²-4x+3及其在点A（1，0）和B（3，0）处的两条切线方程分别为
l₁：2x+y-2=0，l₂：2x-y-6=0
（2）由

y=-2x+2 y=2x-6

可得交点P（2，-2）
S=

∫

2 1

[（x²-4x+3）-（-2x+2）]dx+

∫

3 2

[（x²-4x+3）-（2x-6）]dx
=

∫

2 1

（x²-2x+1）dx+

∫

3 2

(x2-6x+9)dx
=（

1

3

x3-x²+x））

|

2 1

+

1

3

x3-3x²+9

x|

3 2

=

2

3

故选A

点评：本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程、定积分在求面积中的应用等基础知识，考查运算求解能力．属于基础题．