题目内容
数列{an}的前n项和为Sn=10n-n2,求数列{|an|}的前10项和.
解:由an=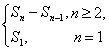 可知an=11-2n,这是一个首项为9,公差为-2的等差数列.
可知an=11-2n,这是一个首项为9,公差为-2的等差数列.
令11-2n>0,得n<5![]() .
.
所以前5项为正,和为S5=5×9+![]() ×(-2)=25.当n≥6时,各项均为
×(-2)=25.当n≥6时,各项均为
负,a6=-1,所以后5项和为5×(-1)+![]() (-2)=-25.
(-2)=-25.
所以数列{|an|}的前10项和为|25|+|-25|=50.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
题目内容
数列{an}的前n项和为Sn=10n-n2,求数列{|an|}的前10项和.
解:由an=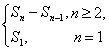 可知an=11-2n,这是一个首项为9,公差为-2的等差数列.
可知an=11-2n,这是一个首项为9,公差为-2的等差数列.
令11-2n>0,得n<5![]() .
.
所以前5项为正,和为S5=5×9+![]() ×(-2)=25.当n≥6时,各项均为
×(-2)=25.当n≥6时,各项均为
负,a6=-1,所以后5项和为5×(-1)+![]() (-2)=-25.
(-2)=-25.
所以数列{|an|}的前10项和为|25|+|-25|=50.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案